یکی از نامساوی های مهم و پرکاربرد در ریاضیات، نامساوی کوشی - شوارتس ( به انگلیسی: Cauchy - Schwarz inequality ) است که به نام های «نامساوی کوشی»، «نامساوی شوارتس»، «نامساوی کوشی - بونیاکوفسکی - شوارتس» و «نامساوی لاگرانژ»[ ۱] نیز مشهور است. علت این نامگذاری ها، شیوه های گوناگون گسترش یافتن این نامساوی به فضاهای مختلف است که در زمینه های مختلفی مانند جبر خطی، آنالیز ریاضی و نظریه احتمالات مطرح می شود. نابرابری کوشی - شوارتز به عنوان یکی از مهم ترین نابرابری های ریاضیات شناخته می شود[ ۲] و به نام آگوستین لویی کوشی و هرمن امندوس شوارتز خوانده می شود.
نابرابری کوشی - شوارتز بیان می کند که برای هر دو بردار دلخواه x و y در فضای ضرب داخلی داریم:
که در آن ⟨ ⋅ , ⋅ ⟩ ضرب داخلی است. هم چنین با گرفتن ریشه دوم طرفین و با توجه به متریک القاء شده توسط این عملگر ضرب داخلی، نامساوی به شکل زیر نوشته می شود:
حالت تساوی رخ می دهد اگر و فقط اگر x و y وابستهٔ خطی باشند.
برای لم تیتو[ ۳] ( همچنین بنام نامساوی برگستورم، فرم انگل یا لم T2 نیز شناخته می شود ) داریم، برای اعداد حقیقی و مثبت داریم:
( ∑ i = 1 n u i ) 2 ∑ i = 1 n v i ≤ ∑ i = 1 n u i 2 v i ≡ u 1 2 v 1 + u 2 2 v 2 + ⋯ + u n 2 v n ≥ ( u 1 + u 2 + ⋯ + u n ) 2 v 1 + v 2 + ⋯ + v n .
برای اثبات کافیست تا ضرب داخلی روی فضای برداری R n را در نظر بگیرید و با جایگذاری u i ′ = u i v i و v i ′ = v i حکم نتیجه می شود.
فضای برداری حقیقی R 2 ، نشان دهنده صفحه دو بعدی است که در آن ضرب داخلی همان حاصل ضرب نقطه ای است. اگر v = ( v 1 , v 2 ) و u = ( u 1 , u 2 ) آنگاه نابرابری کوشی - شوارتز می شود:
⟨ u , v ⟩ 2 = ( ‖ u ‖ ‖ v ‖ cos θ ) 2 ≤ ‖ u ‖ 2 ‖ v ‖ 2 ,
که در آن θ، زاویه بین u و v است.
حالت بالا شاید ساده ترین شکل برای درک نابرابری باشد، زیرا مجذور کسینوس حداکثر می تواند ۱ باشد، که زمانی اتفاق می افتد که بردارها در یک جهت یا مخالف هم باشند. همچنین می توان آن را بر حسب مختصات برداری u 1 , u 2 , v 1 و v 2 تنظیم کرد: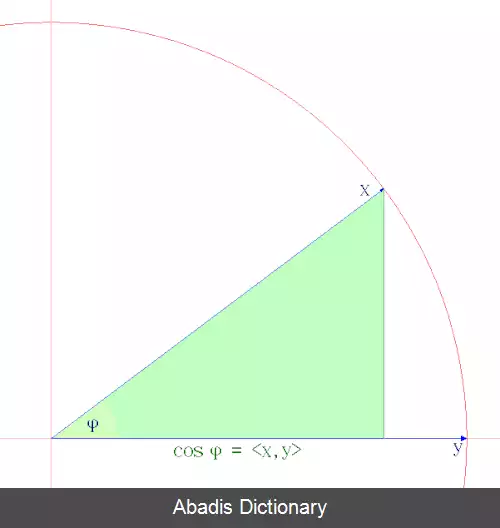
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنابرابری کوشی - شوارتز بیان می کند که برای هر دو بردار دلخواه x و y در فضای ضرب داخلی داریم:
که در آن ⟨ ⋅ , ⋅ ⟩ ضرب داخلی است. هم چنین با گرفتن ریشه دوم طرفین و با توجه به متریک القاء شده توسط این عملگر ضرب داخلی، نامساوی به شکل زیر نوشته می شود:
حالت تساوی رخ می دهد اگر و فقط اگر x و y وابستهٔ خطی باشند.
برای لم تیتو[ ۳] ( همچنین بنام نامساوی برگستورم، فرم انگل یا لم T2 نیز شناخته می شود ) داریم، برای اعداد حقیقی و مثبت داریم:
( ∑ i = 1 n u i ) 2 ∑ i = 1 n v i ≤ ∑ i = 1 n u i 2 v i ≡ u 1 2 v 1 + u 2 2 v 2 + ⋯ + u n 2 v n ≥ ( u 1 + u 2 + ⋯ + u n ) 2 v 1 + v 2 + ⋯ + v n .
برای اثبات کافیست تا ضرب داخلی روی فضای برداری R n را در نظر بگیرید و با جایگذاری u i ′ = u i v i و v i ′ = v i حکم نتیجه می شود.
فضای برداری حقیقی R 2 ، نشان دهنده صفحه دو بعدی است که در آن ضرب داخلی همان حاصل ضرب نقطه ای است. اگر v = ( v 1 , v 2 ) و u = ( u 1 , u 2 ) آنگاه نابرابری کوشی - شوارتز می شود:
⟨ u , v ⟩ 2 = ( ‖ u ‖ ‖ v ‖ cos θ ) 2 ≤ ‖ u ‖ 2 ‖ v ‖ 2 ,
که در آن θ، زاویه بین u و v است.
حالت بالا شاید ساده ترین شکل برای درک نابرابری باشد، زیرا مجذور کسینوس حداکثر می تواند ۱ باشد، که زمانی اتفاق می افتد که بردارها در یک جهت یا مخالف هم باشند. همچنین می توان آن را بر حسب مختصات برداری u 1 , u 2 , v 1 و v 2 تنظیم کرد:

wiki: نابرابری کوشی–شوارتز
