منطق جدایی ( به انگلیسی: Separation Logic ) تعمیمی از منطق هور ( Hoare logic ) است که هدف اصلی ابداع آن، بررسی و وارسی ریاضی برنامه هایی است که داده ها را در حافظه تغییر می دهند و خانه های مختلف از حافظه هستند که در معرض تحول هستند. این منطق توسط جان سی رینولدز, Peter O'Hearn, Samin Ishtiaq و Hongseok Yang معرفی شده است. [ ۱] [ ۲] [ ۳] [ ۴]
در برنامه هایی که از اشاره گر بهره می برند، استفاده از منطق های پیشین نظیر منطق هور ممکن نیست. علت آن است که در این جا، هر خانه از حافظه اهمیت دارد و باید زبان منطق مورد نظر، توانایی اشاره به قسمت های مختلف از حافظهٔ رایانه را داشته باشد. به این دلیل، نیاز به تعریف عملگری جدید حس شد. این احساس نیاز، منجر به تعریف عملگر ∗ شد که به صورت شهودی یعنی دو عملوند آن، در قسمت های مجزا از حافظهٔ پشته هستند؛ لذا، با شکل گیری این منطق و ابزارهای آن، وارسی الگوریتم ها و برنامه های موازی امکان پذیر شده است. [ ۲]
منظور ما در این جا از حالت، وضعیت مقادیر موجود در حافظهٔ تصادفی و همچنین حافظهٔ پشته است. اعلان P در منطق جدایی، تعدادی حالت را مشخص می کند که در آن ها P درست است. با تعریف استقرایی ساختار لغوی منطق جدایی، عبارت P ∗ Q حالاتی را مشخص می کند که P در یک قسمت از ساختار حافظهٔ تصادفی/پشته و Q در قسمتی کاملاً مجزا از آن درست باشد. پس تعریف استقرایی زبان منطق به این صورت است:
• گزارهٔ e m p {\displaystyle \mathbf {e} \mathbf {m} \mathbf {p} } یک پشتهٔ خالی را نشان می دهد. یعنی پشته ای که هیچ خانهٔ آن، به متغیری اختصاص داده نشده باشد.
• عملگر دوتایی ↦ {\displaystyle \mapsto } نشان دهندهٔ یک اشاره گر است. یعنی متغیری به خانه ای از حافظه اشاره می کند.
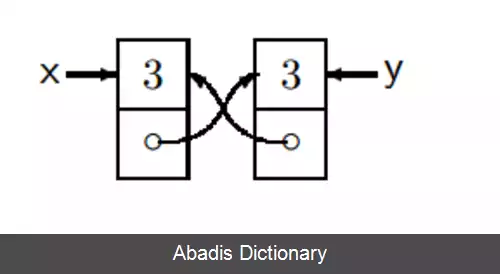
• عملگر دوتایی ∗ {\displaystyle \ast } نشان دهندهٔ درستی دو عبارت در دو قسمت مجزای حافظه است.
• عملگر دوتایی − ∗ {\displaystyle - \!\!\ast } به این معنا است که اگر بتوانیم حافظه را طوری گسترش دهیم که عملگر اول برقرار باشد، عملگر دوم نیز ناگزیر برقرار است. [ ۵]
حال می توان این عملگرها را در مفاهیم منطق مرتبهٔ اول به کار برد و با آن عباراتی در مورد تأثیر یک برنامه بر حافظه گفت یا در بیان مشخصات حافظه استفاده کرد.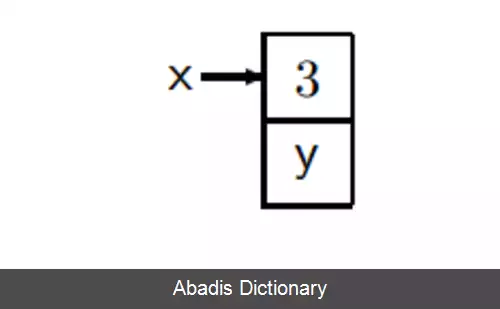
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر برنامه هایی که از اشاره گر بهره می برند، استفاده از منطق های پیشین نظیر منطق هور ممکن نیست. علت آن است که در این جا، هر خانه از حافظه اهمیت دارد و باید زبان منطق مورد نظر، توانایی اشاره به قسمت های مختلف از حافظهٔ رایانه را داشته باشد. به این دلیل، نیاز به تعریف عملگری جدید حس شد. این احساس نیاز، منجر به تعریف عملگر ∗ شد که به صورت شهودی یعنی دو عملوند آن، در قسمت های مجزا از حافظهٔ پشته هستند؛ لذا، با شکل گیری این منطق و ابزارهای آن، وارسی الگوریتم ها و برنامه های موازی امکان پذیر شده است. [ ۲]
منظور ما در این جا از حالت، وضعیت مقادیر موجود در حافظهٔ تصادفی و همچنین حافظهٔ پشته است. اعلان P در منطق جدایی، تعدادی حالت را مشخص می کند که در آن ها P درست است. با تعریف استقرایی ساختار لغوی منطق جدایی، عبارت P ∗ Q حالاتی را مشخص می کند که P در یک قسمت از ساختار حافظهٔ تصادفی/پشته و Q در قسمتی کاملاً مجزا از آن درست باشد. پس تعریف استقرایی زبان منطق به این صورت است:
• گزارهٔ e m p {\displaystyle \mathbf {e} \mathbf {m} \mathbf {p} } یک پشتهٔ خالی را نشان می دهد. یعنی پشته ای که هیچ خانهٔ آن، به متغیری اختصاص داده نشده باشد.
• عملگر دوتایی ↦ {\displaystyle \mapsto } نشان دهندهٔ یک اشاره گر است. یعنی متغیری به خانه ای از حافظه اشاره می کند.
• عملگر دوتایی ∗ {\displaystyle \ast } نشان دهندهٔ درستی دو عبارت در دو قسمت مجزای حافظه است.
• عملگر دوتایی − ∗ {\displaystyle - \!\!\ast } به این معنا است که اگر بتوانیم حافظه را طوری گسترش دهیم که عملگر اول برقرار باشد، عملگر دوم نیز ناگزیر برقرار است. [ ۵]
حال می توان این عملگرها را در مفاهیم منطق مرتبهٔ اول به کار برد و با آن عباراتی در مورد تأثیر یک برنامه بر حافظه گفت یا در بیان مشخصات حافظه استفاده کرد.


wiki: منطق جدایی
