مدارهای ترکیبی، نوعی از مدارهای منطقی هستند که خروجی آن ها در هر لحظه تابع مقادیر ورودی در همان لحظه است. این مدارها در برابر مدارهای ترتیبی مطرح می شوند.
هدف از تحلیل مدارهای ترکیبی، بدست آوردن تابع ( های ) خروجی برحسب متغیرهای ورودی، از روی دیاگرام، است. پس: 1 - نخست، خروجی های همه گیت ها نامگذاری می شوند؛ 2 - تابع های خروجی هر گیت، از طبقه اول، برحسب ورودی های خودش نوشته می شوند؛ 3 - در آخر متغیرهای ورودی جایگزین نام ها می شوند. بنا بر این، برای دیاگرام نمونه داریم: T1=X’YZ T2=XY’Z F=T1+T2=X’YZ+XY’Z
• تعریف مسئله؛
• تعیین تعداد متغیرهای ورودی و تابع های خروجی؛
• تخصیص حروف نمادین به ورودی ها و خروجی ها؛
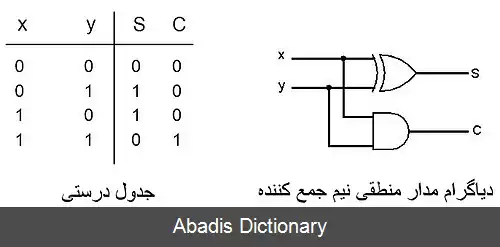
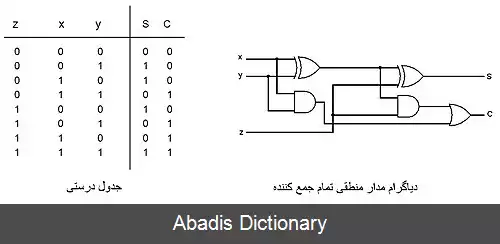
• تشکیل جدول درستی، که رابطهٔ بین ورودی ها و خروجی ها را آشکار می کند؛
• بدست آوردن تابع بول ساده شده برای هر خروجی؛
• رسم مدار منطقی.
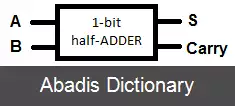
• جمع کننده:
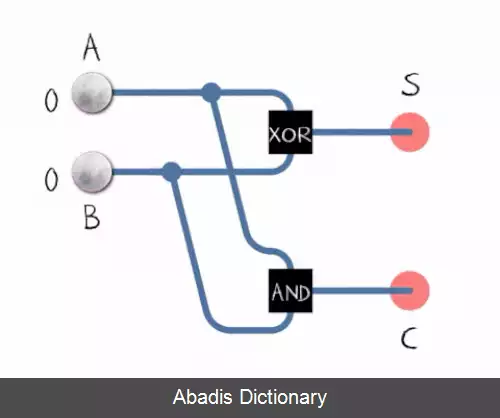
مشاهده می شود که عمل جمع دو عدد تک بیتی توسط 2 گیت AND و XOR قابل انجام است[ ۱]
نحوه کار :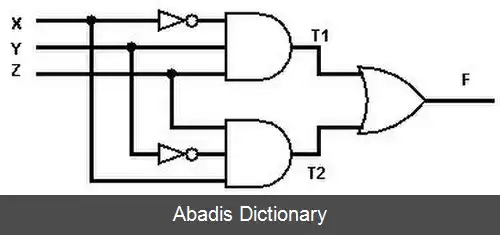
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهدف از تحلیل مدارهای ترکیبی، بدست آوردن تابع ( های ) خروجی برحسب متغیرهای ورودی، از روی دیاگرام، است. پس: 1 - نخست، خروجی های همه گیت ها نامگذاری می شوند؛ 2 - تابع های خروجی هر گیت، از طبقه اول، برحسب ورودی های خودش نوشته می شوند؛ 3 - در آخر متغیرهای ورودی جایگزین نام ها می شوند. بنا بر این، برای دیاگرام نمونه داریم: T1=X’YZ T2=XY’Z F=T1+T2=X’YZ+XY’Z
• تعریف مسئله؛
• تعیین تعداد متغیرهای ورودی و تابع های خروجی؛
• تخصیص حروف نمادین به ورودی ها و خروجی ها؛
• تشکیل جدول درستی، که رابطهٔ بین ورودی ها و خروجی ها را آشکار می کند؛
• بدست آوردن تابع بول ساده شده برای هر خروجی؛
• رسم مدار منطقی.
• جمع کننده:
مشاهده می شود که عمل جمع دو عدد تک بیتی توسط 2 گیت AND و XOR قابل انجام است[ ۱]
نحوه کار :





wiki: منطق ترکیبی
