منحنی های موازی ( Parallel Curves ) ، پوشش یا لفافی از خانواده دایره های هم ارز هستند که حول یک منحنی تمرکز یافته اند. این اشیاء مفهوم خطوط موازی را تعمیم می دهند. همچنین می توان آن را به این صورت نیز تعریف نمود: منحنی که نقاطش در فاصله نرمال ثابتی از یک خم دلخواه قرار داشته باشند. [ ۱]
این دو تعریف کاملاً با هم معادل نیستند، چرا که تعریف اخیر هموار بودن را فرض کرده درحالی که تعریف اولی چنین فرضی را به کار نمی برد. [ ۲]
در طراحی به کمک رایانه ( CAD ) ، اصطلاح منحنی آفست ( Offset Curve ) ترجیح داده می شود. [ ۲] [ ۳] [ ۴]
بر هر نقطه p بر هر منحنی پیوستهٔ c می توان یک خط مماس یکتای t و یک خط نرمال یکتای n رسم کرد. [ ۵] این خط نرمال بر منحنی عمود است و از آن برای اندازه گیری فاصله ها از منحنی استفاده می شود. [ ۶] روی هر خط نرمال n ، تنها دو نقطهٔ q 1 و q 2 هستند که فاصله شان از منحنی c برابر d است. این نقاط را می توان از تقاطع دایره ای به مرکزیت p و با شعاع d و خط نرمال n بدست آورد. [ ۷]
آفست منحنی پیوسته c با فاصلهٔ d به شکل ذیل تعریف می شود: بر روی هر خط نرمال، دو نقطه ای که از منحنی c فاصلهٔ d را داشته باشند مشخص می کنیم. مجموعهٔ همهٔ این نقاط آفست c d است. [ ۸]
به سادگی می توان نشان داد که خط نرمال منحنی آفست c d و منحنی اولیه یکی است، بنابراین خطوط مماس c d و c با هم موازی اند. ازین رو منحنی های آفست منحنی موازی هم نامیده می شوند. [ ۹]
با تغییر دادن فاصلهٔ d می توان خانواده ای از منحنی های آفست بدست آورد. [ ۱۰] برای منحنی های محدب بسته، این آفست ها به دو دسته تقسیم می شوند که یک دسته داخل منحنی و یک دسته بیرون منحنی قرار دارند. [ ۱۱] برای منحنی های باز، دستکم دو روش برای تعریف منحنی آفست وجود دارد: یا آفست ها به شکل دو دستهٔ گسسته تولید می شوند یا می توان آنان را به هم پیوند داد به شکلی که انتهای هر کدام یک نیم دایره باشد. [ ۱۲]
اگر معادله پارامتری یک منحنی مسطح c ( t ) = ( x ( t ) , y ( t ) ) باشد، معادلهٔ پارامتری منحنی آفست آن عبارت است از c d ( t ) = c ( t ) ± d ⋅ n ( t ) که در آن d فاصلهٔ آفست و n ( t ) بردار واحد منحنی نرمال است. برای به دست آوردن n ( t ) منحنی c را ۹۰ درجه می چرخانیم و آن را بر طول خود تقسیم می کنیم:[ ۱۳]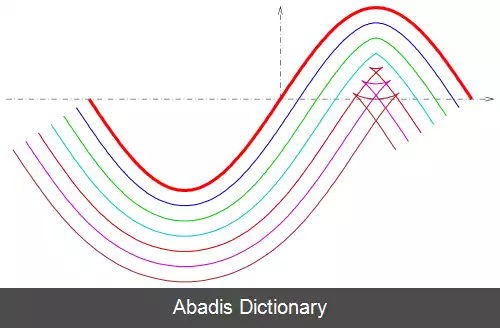
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین دو تعریف کاملاً با هم معادل نیستند، چرا که تعریف اخیر هموار بودن را فرض کرده درحالی که تعریف اولی چنین فرضی را به کار نمی برد. [ ۲]
در طراحی به کمک رایانه ( CAD ) ، اصطلاح منحنی آفست ( Offset Curve ) ترجیح داده می شود. [ ۲] [ ۳] [ ۴]
بر هر نقطه p بر هر منحنی پیوستهٔ c می توان یک خط مماس یکتای t و یک خط نرمال یکتای n رسم کرد. [ ۵] این خط نرمال بر منحنی عمود است و از آن برای اندازه گیری فاصله ها از منحنی استفاده می شود. [ ۶] روی هر خط نرمال n ، تنها دو نقطهٔ q 1 و q 2 هستند که فاصله شان از منحنی c برابر d است. این نقاط را می توان از تقاطع دایره ای به مرکزیت p و با شعاع d و خط نرمال n بدست آورد. [ ۷]
آفست منحنی پیوسته c با فاصلهٔ d به شکل ذیل تعریف می شود: بر روی هر خط نرمال، دو نقطه ای که از منحنی c فاصلهٔ d را داشته باشند مشخص می کنیم. مجموعهٔ همهٔ این نقاط آفست c d است. [ ۸]
به سادگی می توان نشان داد که خط نرمال منحنی آفست c d و منحنی اولیه یکی است، بنابراین خطوط مماس c d و c با هم موازی اند. ازین رو منحنی های آفست منحنی موازی هم نامیده می شوند. [ ۹]
با تغییر دادن فاصلهٔ d می توان خانواده ای از منحنی های آفست بدست آورد. [ ۱۰] برای منحنی های محدب بسته، این آفست ها به دو دسته تقسیم می شوند که یک دسته داخل منحنی و یک دسته بیرون منحنی قرار دارند. [ ۱۱] برای منحنی های باز، دستکم دو روش برای تعریف منحنی آفست وجود دارد: یا آفست ها به شکل دو دستهٔ گسسته تولید می شوند یا می توان آنان را به هم پیوند داد به شکلی که انتهای هر کدام یک نیم دایره باشد. [ ۱۲]
اگر معادله پارامتری یک منحنی مسطح c ( t ) = ( x ( t ) , y ( t ) ) باشد، معادلهٔ پارامتری منحنی آفست آن عبارت است از c d ( t ) = c ( t ) ± d ⋅ n ( t ) که در آن d فاصلهٔ آفست و n ( t ) بردار واحد منحنی نرمال است. برای به دست آوردن n ( t ) منحنی c را ۹۰ درجه می چرخانیم و آن را بر طول خود تقسیم می کنیم:[ ۱۳]

wiki: منحنی موازی
