در ریاضیات و در شاخه ی توپولوژی منحنی سینوسی توپولوژی دانان یک فضای توپولوژیک است با چندین ویژگی قابل توجه که این را به یک مثال مهم تبدیل کرده است. این فضا می تواند به صورت منحنی تابع ( sin ( 1/x تعریف گردد.
T = { ( x , sin 1 x ) : x ∈ ( 0 , 1 ] } ∪ { ( 0 , 0 ) }
این منحنی یک فضای همبند است اما نه به صورت همبند راهی، زیرا اگرچه دارای نقطه ( ۰, ۰ ) است اما نمی توان تابع را مرتبط کرد تا راهی ایجاد شود.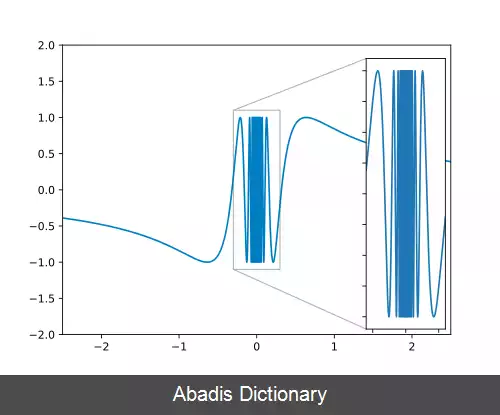
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفT = { ( x , sin 1 x ) : x ∈ ( 0 , 1 ] } ∪ { ( 0 , 0 ) }
این منحنی یک فضای همبند است اما نه به صورت همبند راهی، زیرا اگرچه دارای نقطه ( ۰, ۰ ) است اما نمی توان تابع را مرتبط کرد تا راهی ایجاد شود.

