در الکترونیک، مقسم جریان یک مدار خطی ساده است که یک جریان خروجی ( I X ) که کسری از جریان ورودی اش ( I T ) است، تولید می کند. تقسیم جریان به تقسیم جریان بین شاخه های تقسیم اشاره دارد. جریان ها در شاخه های مختلف چنین مداری همیشه به گونه ای تقسیم می شوند تا انرژی مصرفی کل به حداقل برسد.
فرمول مقسم جریان تقریباً مشابه به شکل مقسم ولتاژ است. هرچند، نسبت توصیف کننده تقسیم جریان، امپدانس شاخه های در نظر گرفته شده را بر خلاف تقسیم ولتاژ که امپدانس های در نظر گرفته شده را در صورت قرار می دهد در مخرج قرار می دهد. به این دلیل است که در مقسم های جریان، کل انرژی مصرفی حداقل شده، و در نتیجه جریان هایی که از طریق مسیرهای کم امپدانس عبور می کنند، به این دلیل رابطه معکوس با امپدانس دارند. از سوی دیگر مقسم ولتاژ برای تصدیق قانون ولتاژ کیرشهف استفاده می شود. مجموع ولتاژ دور تا دور یک حلقه باید صفر بشود، بنابراین افت ولتاژ باید به طور مساوی در رابطه مستقیم با امپدانس تقسیم شود.
به طور خاص اگر دو یا چند امپدانس موازی باشند، جریانی که وارد ترکیب می شود بین آنها در نسبت معکوس با امپدنس هایشان ( با توجه به قانون اهم ) تقسیم خواهد شد. همچنین استنباط می شود که اگر امپدانس ها مقداری برابر داشته باشند جریان به طور مساوی تقسیم می شود.
یک فرمول کلی برای جریان I X در مقاومت R X که موازی با یک ترکیب دیگر از مقاومت ها از مقامت کل RT است ( به شکل ۱ نگاه کنید ) :
که I T جریان کل ورودی به شبکه ترکیبی R X به موازات R T است. توجه کنید که وقتی R T از یک ترکیب موازی از مقاومت تشکیل شده باشد، می گوییم R 1، R 2، … و غیره، پس باید معکوس هر مقاومت برای پیدا کردن مقامت کل R Tباهم جمع شوند :
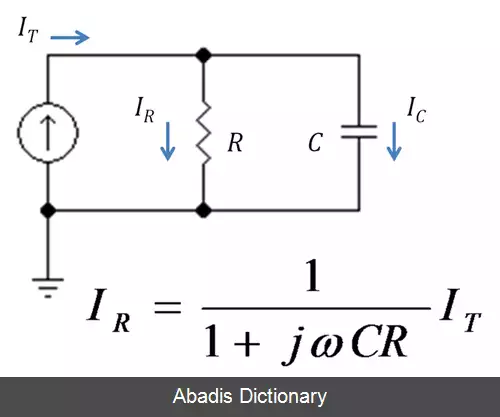
اگر چه مقسم مقاومت رایج است، مقسم جریان ممکن است از امپدانسهای وابسته به فرکانس ساخته شود. در حالت کلی جریان IX داده شده است:
که در آن ZT اشاره به امپدانس معادل کل مدار دارد.
به جای استفاده از امپدانس ها، اگر ادمیتانس ( معکوس امپدانس ) مورد استفاده قرار گیرد، قانون مقسم جریان می تواند همانند قانون مقسم ولتاژ استفاده شود.
توجه داشته باشید که Y Total یک جمع ساده است، نه معکوس شدهٔ مجموع معکوس ها ( همان طور که برای یک شبکه معمولی مقاومتی موازی انجام می دهید ) . برای شکل ۱، جریان I X این چنین خواهد بود
I X = Y X Y T o t a l I T = 1 R X 1 R X + 1 R 1 + 1 R 2 + 1 R 3 I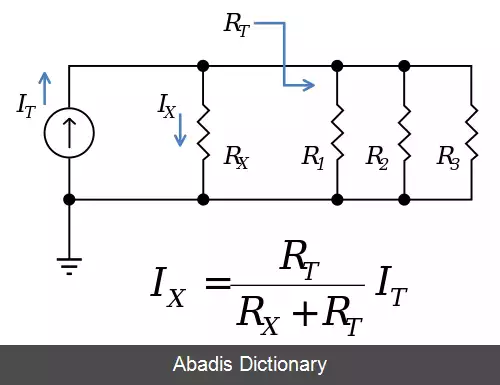
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرمول مقسم جریان تقریباً مشابه به شکل مقسم ولتاژ است. هرچند، نسبت توصیف کننده تقسیم جریان، امپدانس شاخه های در نظر گرفته شده را بر خلاف تقسیم ولتاژ که امپدانس های در نظر گرفته شده را در صورت قرار می دهد در مخرج قرار می دهد. به این دلیل است که در مقسم های جریان، کل انرژی مصرفی حداقل شده، و در نتیجه جریان هایی که از طریق مسیرهای کم امپدانس عبور می کنند، به این دلیل رابطه معکوس با امپدانس دارند. از سوی دیگر مقسم ولتاژ برای تصدیق قانون ولتاژ کیرشهف استفاده می شود. مجموع ولتاژ دور تا دور یک حلقه باید صفر بشود، بنابراین افت ولتاژ باید به طور مساوی در رابطه مستقیم با امپدانس تقسیم شود.
به طور خاص اگر دو یا چند امپدانس موازی باشند، جریانی که وارد ترکیب می شود بین آنها در نسبت معکوس با امپدنس هایشان ( با توجه به قانون اهم ) تقسیم خواهد شد. همچنین استنباط می شود که اگر امپدانس ها مقداری برابر داشته باشند جریان به طور مساوی تقسیم می شود.
یک فرمول کلی برای جریان I X در مقاومت R X که موازی با یک ترکیب دیگر از مقاومت ها از مقامت کل RT است ( به شکل ۱ نگاه کنید ) :
که I T جریان کل ورودی به شبکه ترکیبی R X به موازات R T است. توجه کنید که وقتی R T از یک ترکیب موازی از مقاومت تشکیل شده باشد، می گوییم R 1، R 2، … و غیره، پس باید معکوس هر مقاومت برای پیدا کردن مقامت کل R Tباهم جمع شوند :
اگر چه مقسم مقاومت رایج است، مقسم جریان ممکن است از امپدانسهای وابسته به فرکانس ساخته شود. در حالت کلی جریان IX داده شده است:
که در آن ZT اشاره به امپدانس معادل کل مدار دارد.
به جای استفاده از امپدانس ها، اگر ادمیتانس ( معکوس امپدانس ) مورد استفاده قرار گیرد، قانون مقسم جریان می تواند همانند قانون مقسم ولتاژ استفاده شود.
توجه داشته باشید که Y Total یک جمع ساده است، نه معکوس شدهٔ مجموع معکوس ها ( همان طور که برای یک شبکه معمولی مقاومتی موازی انجام می دهید ) . برای شکل ۱، جریان I X این چنین خواهد بود
I X = Y X Y T o t a l I T = 1 R X 1 R X + 1 R 1 + 1 R 2 + 1 R 3 I




wiki: مقسم جریان
