بعضی از مقدارهای مثلثاتی را می توان به صورت عبارت های جبری دقیق به دست آورد و در ساده کردن عبارت های ریاضی از آن ها استفاده کرد. همه مقدارهای مثلثاتی برای زاویه °۳ و همه مضرب های آن به صورت دقیق، قابل محاسبه است. هم چنین با استفاده از اتحادهای زاویه ۳ برابر، می توان مقدارهای مثلثاتی را برای زاویه °۱ به دست آورد. به این ترتیب، نسبت های مثلثاتی برای همه زاویه ها به دست می آید.
در برخی از زاویه ها مقدار دقیق برای همه تابع های مثلثاتی وجود دارد. ولی در بعضی از آن ها، مقدار دقیق برای بعضی از تابع ها دارای رابطه بسیار پیچیده ای است.
در جدول زیر، مقدارهای دقیق سینوس، کسینوس و تانژانت برای زاویه های صفر تا °۴۵ ارائه شده است. برای زاویه های بزرگتر، می توان با استفاده از اتحادهای مثلثاتی متناظر، مقدار مورد نظر را به دست آورد. هم چنین سایر نسبت ها معکوس سه تابع اصلی هستند و با معلوم بودن تابع های اصلی، به سادگی قابل محاسبه می باشند.
برای زاویه های بین ۴۵ تا ۹۰ درجه، از رابطه های مربوط به زاویه متمم استفاده می شود. برای زاویه های بزرگتر از ۹۰ درجه نیز اتحادهای دوران مثلثاتی به کار گرفته می شوند.
برای چند زاویه به جز زاویه های جدول بالا، مقدار دقیق وجود دارد؛ ولی عبارت های ریاضی بسیار پیچیده ای برای تانژانت به دست می آید. به همین دلیل، تنها مقدار سینوس و کسینوس این زاویه ها در جدول زیر نشان داده می شود.
نسبت های مثلثاتی برای زاویه های ۳۰ و ۶۰ درجه با مثلث متساوی الاضلاع و برای زاویه ۴۵ درجه با مثلث متساوی الساقین به دست می آید.
دو روش هندسی و جبری برای محاسبه نسبت های مثلثاتی زاویه °۳۶ وجود دارد.
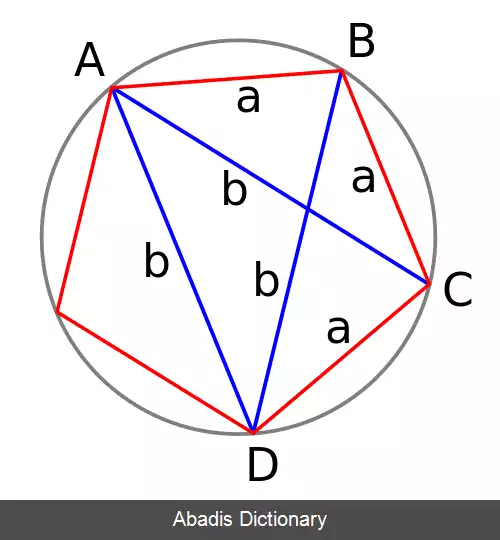
یک پنج ضلعی منتظم مشابه شکل روبرو، دارای پنج زاویه °۱۰۸ است. زیرا جمع زاویه های پنج ضلعی برابر °۵۴۰= ( ۲ - ۵ ) ×۱۸۰ است. هم چنین زاویه کمان بین هر دو رأس متوالی برابر °۷۲=۵÷۳۶۰ است. بنابراین از آن جایی که زاویه محاطی نصف کمان روبرو است، [ ۱] مقدار زاویه ADB برابر °۳۶ است.
از سوی دیگر، بر پایه قضیه بطلمیوس، می توان نشان داد که در پنج ضلعی منتظم رابطه b2=a2+ab برقرار است. ( a اندازه ضلع و b اندازه قطر پنج ضلعی است. ) با حل پارامتری این معادله، رابطه زیر به دست می آید که به نسبت طلایی معروف است:
می توان نشان داد که رابطه زیر، میان زاویه بین دو ساق ( θ ) و ضلع های یک مثلث متساوی الساقین ( شامل ساق b و قاعده a ) وجود دارد: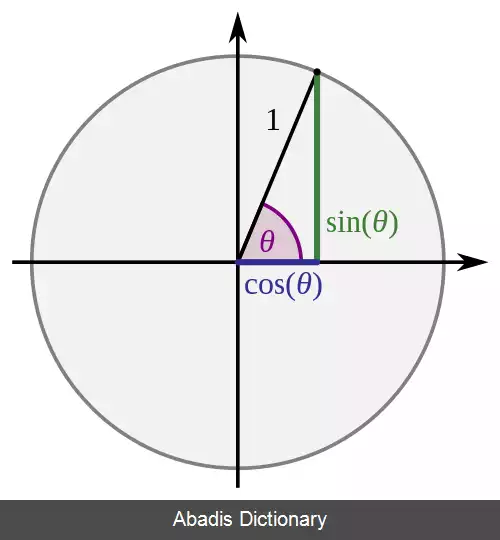
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر برخی از زاویه ها مقدار دقیق برای همه تابع های مثلثاتی وجود دارد. ولی در بعضی از آن ها، مقدار دقیق برای بعضی از تابع ها دارای رابطه بسیار پیچیده ای است.
در جدول زیر، مقدارهای دقیق سینوس، کسینوس و تانژانت برای زاویه های صفر تا °۴۵ ارائه شده است. برای زاویه های بزرگتر، می توان با استفاده از اتحادهای مثلثاتی متناظر، مقدار مورد نظر را به دست آورد. هم چنین سایر نسبت ها معکوس سه تابع اصلی هستند و با معلوم بودن تابع های اصلی، به سادگی قابل محاسبه می باشند.
برای زاویه های بین ۴۵ تا ۹۰ درجه، از رابطه های مربوط به زاویه متمم استفاده می شود. برای زاویه های بزرگتر از ۹۰ درجه نیز اتحادهای دوران مثلثاتی به کار گرفته می شوند.
برای چند زاویه به جز زاویه های جدول بالا، مقدار دقیق وجود دارد؛ ولی عبارت های ریاضی بسیار پیچیده ای برای تانژانت به دست می آید. به همین دلیل، تنها مقدار سینوس و کسینوس این زاویه ها در جدول زیر نشان داده می شود.
نسبت های مثلثاتی برای زاویه های ۳۰ و ۶۰ درجه با مثلث متساوی الاضلاع و برای زاویه ۴۵ درجه با مثلث متساوی الساقین به دست می آید.
دو روش هندسی و جبری برای محاسبه نسبت های مثلثاتی زاویه °۳۶ وجود دارد.
یک پنج ضلعی منتظم مشابه شکل روبرو، دارای پنج زاویه °۱۰۸ است. زیرا جمع زاویه های پنج ضلعی برابر °۵۴۰= ( ۲ - ۵ ) ×۱۸۰ است. هم چنین زاویه کمان بین هر دو رأس متوالی برابر °۷۲=۵÷۳۶۰ است. بنابراین از آن جایی که زاویه محاطی نصف کمان روبرو است، [ ۱] مقدار زاویه ADB برابر °۳۶ است.
از سوی دیگر، بر پایه قضیه بطلمیوس، می توان نشان داد که در پنج ضلعی منتظم رابطه b2=a2+ab برقرار است. ( a اندازه ضلع و b اندازه قطر پنج ضلعی است. ) با حل پارامتری این معادله، رابطه زیر به دست می آید که به نسبت طلایی معروف است:
می توان نشان داد که رابطه زیر، میان زاویه بین دو ساق ( θ ) و ضلع های یک مثلث متساوی الساقین ( شامل ساق b و قاعده a ) وجود دارد:


wiki: مقدارهای دقیق مثلثاتی
