در ریاضیات، یک گراف چگال گرافی است که تعداد یال های آن نزدیک به بیشینه تعداد یال ها باشد. درمقابل یک گراف با کمینه تعداد یال ها یک گراف اسپارس است. تمایز بین گراف اسپارس و چگال مبهم است و بستگی به محتوای آن ها دارد. برای گراف بدون جهت ساده، گراف چگال به صورت روبرو تعریف می شود: D = 2 | E | | V | ( | V | − 1 ) بیشینه تعداد یال ها | V | ( | V | − 1 ) 2 است بنابراین چگالی ماکسیمال آن ۱ می باشد . اما برای گراف جهتدار چگالی به صورت زیر تعریف می شود:
D = | E | | V | ( | V | − 1 )
اگر گراف G = ( V , E ) را در نظر بگیریم:
در گراف اسپارس | E | = O ( | V | ) . و در گراف چگال | E | = Θ ( | V | 2 ) .
گراف G = ( V , E ) ، با n راس را در نظر بگیرید. فرض کنید درجهٔ خروجی هر رأس در گراف G، مقدار ثابت K باشد. می گوییم گراف G اسپارس است زیرا | E | = k | V | = O ( | V | ) .
اگر فرض کنیم که درجهٔ خروجی هر رأس در گراف G، مقدار اعشاری f بین ۰ و ۱ باشد. مثلا اگر n = ۱۶ و f = ۰٫۲۵، درجهٔ خروجی هر رأس ۴است. آن گاه گراف G چگال است زیرا | E | = f | V | 2 = Θ ( | V | 2 ) .
شکل ۱: یک گراف خطی که هر راس دارای دو لبهٔ متقاطع است.
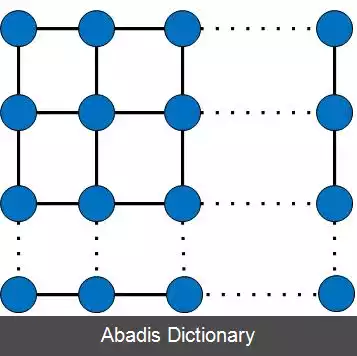
شکل ۲:یک گراف شبکه در آن هر راس دارای چهار لبهٔ متقاطع است.
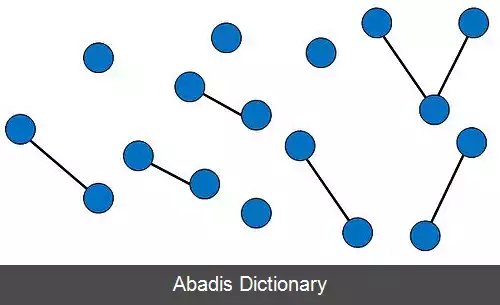
شکل ۳:یک گراف تصادفی اسپارس
طبق تعریف استرینو و تران :
• یک گراف ( k, I ) – اسپارس است اگر تمام زیرگراف های غیرتهی با n راس آن دارای حداکثر kn - I یال باشند.
• یک گراف ( k, I ) - متراکم است اگر ( k, I ) - اسپارس باشد و دقیقا kn - I یال داشته باشد.
مثال
سایر خانواده های گراف که توسط پراکندگیشان قابل طبقه بندی نیستند، می توان به صورت زیر توصیف کرد:
به عنوان مثال هر گراف مسطح با n راس دارای حداکثر ۳n - ۶ یال است. هر زیرگراف گراف مسطح، مسطح است. بنابراین گراف های مسطح ( ۶و۳ ) - اسپارس هستند اما هر گراف ( ۶و۳ ) - اسپارس، لزوما مسطح نیست. به طور مشابه گراف های مسطح بیرونی ( ۳و۲ ) - اسپارس و گراف های مسطح دوبخشی ( ۴و۲ ) - اسپارس هستند. استرینو و تران نشان داد که امتحان کردن پراکندگی ( K, I ) ممکن است در زمان چندجمله ای اجرا شود.
فراچگالی گسترش یافتهٔ مفهوم چگالی گراف بر روی گراف های متناهی تا گراف های نامتناهی می باشد . به طور مستقیم، یک گراف متناهی ذاتا دارای زیرگراف های محدود بزرگ با چگالی کم تر از فراچگالی خود هستند، و ذاتا فاقد زیرگراف های محدود بزرگتر از فراچگالی خود می باشند. به عبارت دیگر، فراچگالی گراف G، بزرگترین کرانه پایین ( Infimum ) مقادیر a ای است که زیرگراف های متناهی G با چگالی a دارای تعداد رئوس متناهی باشند. با استفاده از قضیهٔ اردوس - استون می توان نشان داد که فراچگالی می تواند تنها ۱و یا یکی از نسبت های ویژه ی۰، ۱/۲، ۲/۳، ۳/۴، ۴/۵، . . . ، ( n/ ( n+1، . . . . باشد.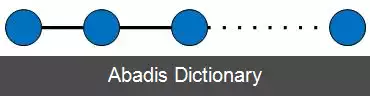
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفD = | E | | V | ( | V | − 1 )
اگر گراف G = ( V , E ) را در نظر بگیریم:
در گراف اسپارس | E | = O ( | V | ) . و در گراف چگال | E | = Θ ( | V | 2 ) .
گراف G = ( V , E ) ، با n راس را در نظر بگیرید. فرض کنید درجهٔ خروجی هر رأس در گراف G، مقدار ثابت K باشد. می گوییم گراف G اسپارس است زیرا | E | = k | V | = O ( | V | ) .
اگر فرض کنیم که درجهٔ خروجی هر رأس در گراف G، مقدار اعشاری f بین ۰ و ۱ باشد. مثلا اگر n = ۱۶ و f = ۰٫۲۵، درجهٔ خروجی هر رأس ۴است. آن گاه گراف G چگال است زیرا | E | = f | V | 2 = Θ ( | V | 2 ) .
شکل ۱: یک گراف خطی که هر راس دارای دو لبهٔ متقاطع است.
شکل ۲:یک گراف شبکه در آن هر راس دارای چهار لبهٔ متقاطع است.
شکل ۳:یک گراف تصادفی اسپارس
طبق تعریف استرینو و تران :
• یک گراف ( k, I ) – اسپارس است اگر تمام زیرگراف های غیرتهی با n راس آن دارای حداکثر kn - I یال باشند.
• یک گراف ( k, I ) - متراکم است اگر ( k, I ) - اسپارس باشد و دقیقا kn - I یال داشته باشد.
مثال
سایر خانواده های گراف که توسط پراکندگیشان قابل طبقه بندی نیستند، می توان به صورت زیر توصیف کرد:
به عنوان مثال هر گراف مسطح با n راس دارای حداکثر ۳n - ۶ یال است. هر زیرگراف گراف مسطح، مسطح است. بنابراین گراف های مسطح ( ۶و۳ ) - اسپارس هستند اما هر گراف ( ۶و۳ ) - اسپارس، لزوما مسطح نیست. به طور مشابه گراف های مسطح بیرونی ( ۳و۲ ) - اسپارس و گراف های مسطح دوبخشی ( ۴و۲ ) - اسپارس هستند. استرینو و تران نشان داد که امتحان کردن پراکندگی ( K, I ) ممکن است در زمان چندجمله ای اجرا شود.
فراچگالی گسترش یافتهٔ مفهوم چگالی گراف بر روی گراف های متناهی تا گراف های نامتناهی می باشد . به طور مستقیم، یک گراف متناهی ذاتا دارای زیرگراف های محدود بزرگ با چگالی کم تر از فراچگالی خود هستند، و ذاتا فاقد زیرگراف های محدود بزرگتر از فراچگالی خود می باشند. به عبارت دیگر، فراچگالی گراف G، بزرگترین کرانه پایین ( Infimum ) مقادیر a ای است که زیرگراف های متناهی G با چگالی a دارای تعداد رئوس متناهی باشند. با استفاده از قضیهٔ اردوس - استون می توان نشان داد که فراچگالی می تواند تنها ۱و یا یکی از نسبت های ویژه ی۰، ۱/۲، ۲/۳، ۳/۴، ۴/۵، . . . ، ( n/ ( n+1، . . . . باشد.




