در الکترونیک، معیار پایداری بارک هاوزن ( به انگلیسی: Barkhausen stability criterion ) یک شرط ریاضی برای تعیین این است که درچه صورت یک مدار الکترونیکی خطی نوسان خواهدکرد. [ ۱] [ ۲] [ ۳] این معیار درسال ۱۹۲۱ توسط فیزیک دان آلمانی هاینریش گئورگ بارک هاوزن ( ۱۸۸۱–۱۹۵۶ ) مطرح شد. [ ۴] ین معیار، برای جلوگیری از نوسان کردن مدارهای الکتریکی دارای بازخورد منفی، مانند مدارهای آمپ اَمپی، و در طراحی نوسان سازها، کاربرد زیادی دارد.
معیار بارک هاوزن در طراحی مدارهای خطی دارای بازخورد به میان می آید. نمی توان آن را مستقیماً روی عناصر فعال با مقاومت منفی مانند نوسان سازهای دیود تونلی اعمال کرد.
در نوسان پایدار، یک جفت قطب باید روی محور موهومی صفحه فرکانس مختلط قرار دارد. درعمل، پایدار ماندن نوسان ساز، با قرار داشتن قطب ها روی محور موهومی ناممکن است؛ بنابراین، در یک نوسان ساز پایدار، دو شرط زیر باید برقرار شوند؛
• بازخورد مثبت
• بهره حلقهٔ برابر با یک باشد ( | β A | = 1 {\displaystyle |\beta A|=1\, } ) .
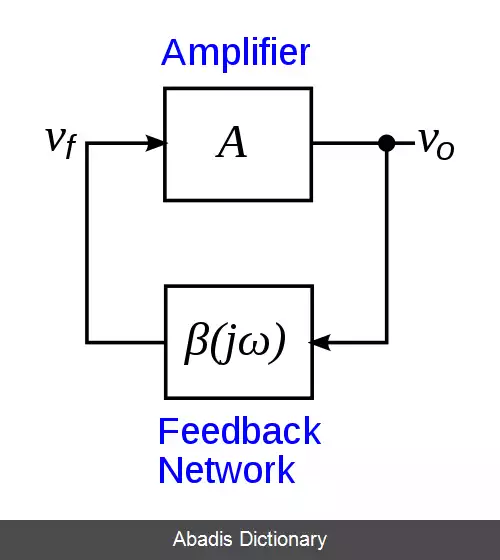
اگر بهره تقویت کننده در مدار، A، و تابع انتقال مسیر بازخورد، β ( j ω ) باشد، بهره حلقه، βA است. نوسان مدار، تنها در فرکانسی پایدار خواهد بود که:
• قدر مطلق بهره حلقه برابر واحد باشد؛ | β A | = 1 {\displaystyle |\beta A|=1\, }
• فاز بهره حلقه، صفر یا مضربی از ۲π باشد؛ ∠ β A = 2 π n , n ∈ { 0 , 1 , 2 , … } {\displaystyle \angle \beta A=2\pi n, n\in \{0, 1, 2, \dots \}}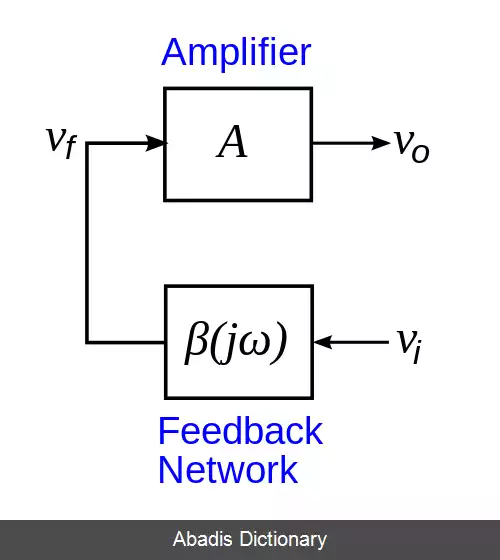
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمعیار بارک هاوزن در طراحی مدارهای خطی دارای بازخورد به میان می آید. نمی توان آن را مستقیماً روی عناصر فعال با مقاومت منفی مانند نوسان سازهای دیود تونلی اعمال کرد.
در نوسان پایدار، یک جفت قطب باید روی محور موهومی صفحه فرکانس مختلط قرار دارد. درعمل، پایدار ماندن نوسان ساز، با قرار داشتن قطب ها روی محور موهومی ناممکن است؛ بنابراین، در یک نوسان ساز پایدار، دو شرط زیر باید برقرار شوند؛
• بازخورد مثبت
• بهره حلقهٔ برابر با یک باشد ( | β A | = 1 {\displaystyle |\beta A|=1\, } ) .
اگر بهره تقویت کننده در مدار، A، و تابع انتقال مسیر بازخورد، β ( j ω ) باشد، بهره حلقه، βA است. نوسان مدار، تنها در فرکانسی پایدار خواهد بود که:
• قدر مطلق بهره حلقه برابر واحد باشد؛ | β A | = 1 {\displaystyle |\beta A|=1\, }
• فاز بهره حلقه، صفر یا مضربی از ۲π باشد؛ ∠ β A = 2 π n , n ∈ { 0 , 1 , 2 , … } {\displaystyle \angle \beta A=2\pi n, n\in \{0, 1, 2, \dots \}}


wiki: معیار پایداری بارک هاوزن
