معیار ISI نایکویست. در مخابرات، معیار تداخل میان سمبلی نایکویست ( Nyquist Intersymbol Interference, ISI ) شرایطی را توصیف می کند که وقتی ازسوی یک کانال مخابراتی ( شامل پاسخ فیلترهای فرستنده و گیرنده ) برآورده شوند، تداخل میان سمبلی ( ISI ) روی نمی دهد. این معیار، روشی برای طراحی توابع محدودباند ( band - limited ) برای غلبه بر تداخل میان نمادی پیش می نهد.
هنگامی که سمبل های پشت ِهم، روی یک کانال از راه یک مدولاسیون خطی ( مانند ASK ، QAM ) منتقل می شوند، پاسخ ضربه کانال ( یا معادل آن، پاسخ فرکانسی کانال ) باعث می شود که سمبل های ارسال شده، در حوزه زمان پخش شوند. این باعث تداخل میان سمبلی می شود زیرا سمبل های ارسال شدۀ پیشین، بر سمبل دریافت شدۀ کنونی اثر می گذارند و بنابراین آستانه تحمل نویز در سیستم را کاهش می دهد. قضیه نایکویست، این وضعیت در حوزه زمان را به یک وضعیت در دامنه فرکانس معادل، مرتبط می کند.
معیار نایکویست ارتباط نزدیکی با قضیه نمونه برداری نایکویست - شانون دارد، تنها از دیدگاهی دیگر.
اگر پاسخ ضربه کانال را با h ( t ) نشان دهیم، شرط یک پاسخ بدون ISI را می توان چنین بیان کرد:
برای همه اعداد صحیح n ، و T s ، دورۀ سمبل است. قضیه نایکویست می گوید که این معادل است با:
که H ( f ) تبدیل فوریۀ h ( t ) است . این معیار ISI نایکویست است.
این معیار را می توان شهودی چنین درک کرد: ک مقدار ثابت باید به نسخه های شیفت ِفرکانسی یافتۀ H ( f ) افزوده شود. این شرط وقتی برقرار می شود که H ( f ) ، تقارن یکنواخت دارد، پهنای باند کمتر یا مساوی 2 / T s دارد، و باند تک جانبی آن در فرکانس قطع ± 1 / 2 T s ، تقارن فرد دارد .
در عمل، این معیار در فرستنده، در مرحلۀ فیلترکردن سمبل های باندِ پایه و با درنظرگرفتن دنبالۀ سمبل ها به عنوان پالس های وزن دار ( تابع دلتای دیراک ) اعمال می شود. هنگامی که فیلتر باند پایه، معیار نایکویست را برمی آورد، می توان سمبل ها را بدون ISI از کانالی که پاسخ فرکانسی اش در یک باند فرکانسی محدود، تخت است، منتقل کرد. نمونه هایی از این فیلتر باند پایه، فیلتر کسینوس بالابرده ( raised cosine ) ، یا فیلتر پایین گذر ایدئال هستند.
برای به دست آوردن این معیار، سیگنال دریافت شده را بر حسب سمبل ارسالی و پاسخ کانال بیان می کنیم. اگر h ( t ) پاسخ ضربه کانال باشد، x سمبل هایی با دورۀ T s هستند که باید ارسال شوند. سیگنال دریافت شده y ( t ) - که برای سادگی، نویز در آن نادیده گرفته شده است - چنین خواهد بود: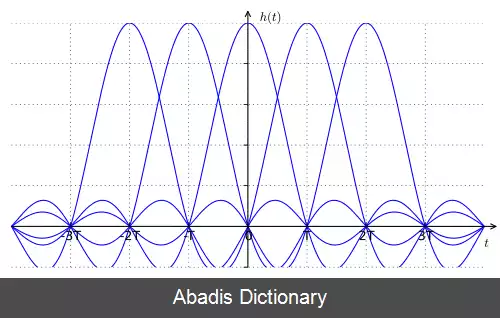
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهنگامی که سمبل های پشت ِهم، روی یک کانال از راه یک مدولاسیون خطی ( مانند ASK ، QAM ) منتقل می شوند، پاسخ ضربه کانال ( یا معادل آن، پاسخ فرکانسی کانال ) باعث می شود که سمبل های ارسال شده، در حوزه زمان پخش شوند. این باعث تداخل میان سمبلی می شود زیرا سمبل های ارسال شدۀ پیشین، بر سمبل دریافت شدۀ کنونی اثر می گذارند و بنابراین آستانه تحمل نویز در سیستم را کاهش می دهد. قضیه نایکویست، این وضعیت در حوزه زمان را به یک وضعیت در دامنه فرکانس معادل، مرتبط می کند.
معیار نایکویست ارتباط نزدیکی با قضیه نمونه برداری نایکویست - شانون دارد، تنها از دیدگاهی دیگر.
اگر پاسخ ضربه کانال را با h ( t ) نشان دهیم، شرط یک پاسخ بدون ISI را می توان چنین بیان کرد:
برای همه اعداد صحیح n ، و T s ، دورۀ سمبل است. قضیه نایکویست می گوید که این معادل است با:
که H ( f ) تبدیل فوریۀ h ( t ) است . این معیار ISI نایکویست است.
این معیار را می توان شهودی چنین درک کرد: ک مقدار ثابت باید به نسخه های شیفت ِفرکانسی یافتۀ H ( f ) افزوده شود. این شرط وقتی برقرار می شود که H ( f ) ، تقارن یکنواخت دارد، پهنای باند کمتر یا مساوی 2 / T s دارد، و باند تک جانبی آن در فرکانس قطع ± 1 / 2 T s ، تقارن فرد دارد .
در عمل، این معیار در فرستنده، در مرحلۀ فیلترکردن سمبل های باندِ پایه و با درنظرگرفتن دنبالۀ سمبل ها به عنوان پالس های وزن دار ( تابع دلتای دیراک ) اعمال می شود. هنگامی که فیلتر باند پایه، معیار نایکویست را برمی آورد، می توان سمبل ها را بدون ISI از کانالی که پاسخ فرکانسی اش در یک باند فرکانسی محدود، تخت است، منتقل کرد. نمونه هایی از این فیلتر باند پایه، فیلتر کسینوس بالابرده ( raised cosine ) ، یا فیلتر پایین گذر ایدئال هستند.
برای به دست آوردن این معیار، سیگنال دریافت شده را بر حسب سمبل ارسالی و پاسخ کانال بیان می کنیم. اگر h ( t ) پاسخ ضربه کانال باشد، x سمبل هایی با دورۀ T s هستند که باید ارسال شوند. سیگنال دریافت شده y ( t ) - که برای سادگی، نویز در آن نادیده گرفته شده است - چنین خواهد بود:

wiki: معیار ISI نایکویست
