معادله آورامی. معادله آورامی توضیح می دهد که چگونه جامدات در دمای ثابت از یک فاز به فاز دیگر تبدیل می شوند. این می تواند به طور خاص سینتیک تبلور را توصیف کند، می تواند به طور کلی برای سایر تغییرات فاز در مواد مانند سرعت واکنش شیمیایی اعمال شود، و حتی می تواند در تجزیه و تحلیل سیستم های اکولوژیکی کاربرد داشته باشد. [ ۱]
این معادله با نام معادله جانسون – مهل – اورامی – کلموگروف ( JMAK ) نیز شناخته می شود. این معادله برای اولین بار توسط جانسون، مهل، اورامی و کولموگروف ( به زبان روسی ) در مجموعه ای از مقالات منتشر شده در مجله فیزیک شیمی بین سال های 1939 و 1941 استخراج شده است. [ ۲] [ ۳] [ ۴] علاوه بر این، کولموگروف از نظر آماری تبلور یک جامد را در سال 1937 بررسی کرد ( به روسی، Kolmogorov، AN، Izv. آکاد. ناوک. SSSR. , 1937, 3, 355 ) .
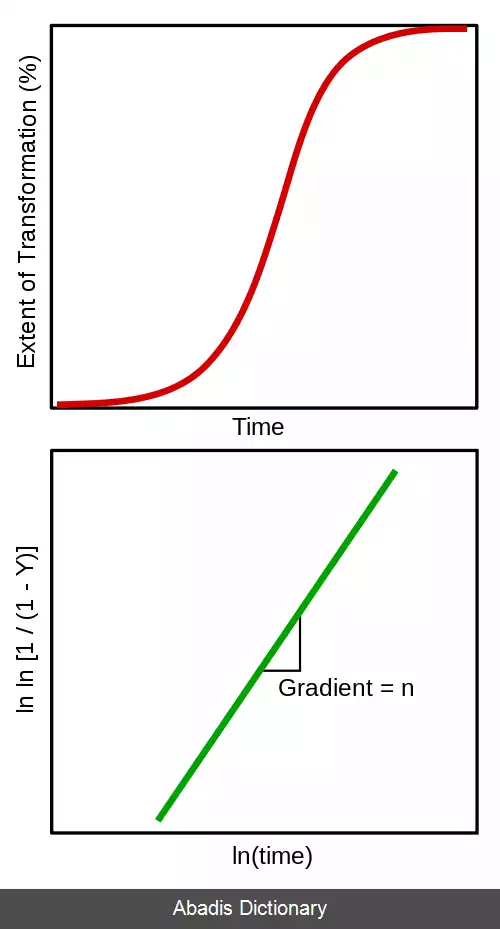
تغییرات اغلب یک روند s شکل یا سیگموئیدی را طی می کنند که در آن نرخ تبدیل در ابتدا و انتهای تبدیل کم است، اما در بین آن ها سریع است.
سرعت آهسته در مراحل اول را می توان به زمان مورد نیاز برای تشکیل و شروع رشد تعداد قابل توجهی از هسته های فاز جدید نسبت داد. در طول دوره میانی، سرعت تبدیل سریع است زیرا هسته ها به ذرات تبدیل می شوند و فاز قدیمی را مصرف می کنند در حالی که هسته ها در فاز اصلی باقی مانده به شکل گیری ادامه می دهند.
هنگامی که تبدیل به مراحل نهایی نزدیک می شود، مواد تغییر نیافته کمی برای هسته سازی بیشتر باقی می ماند و تولید ذرات جدید شروع به کند شدن می کند. علاوه بر این، ذرات تشکیل شده قبلی شروع به تماس با یکدیگر می کنند و مرزی را تشکیل می دهند که در آن رشد متوقف می شود.
برای استخراج ساده ترین حالت معادله آورامی تعداد قابل توجهی فرض و ساده سازی را ایجاد می کند: [ ۵]
• هسته زایی به طور تصادفی و همگن در کل بخش تبدیل نشده ماده رخ می دهد.
• نرخ رشد به میزان استحاله فازی بستگی ندارد.
• رشد در همه جهات با سرعت یکسان اتفاق می افتد.
اگر این شرایط برآورده شود، تغییر فاز α به β با هسته زایی ذرات جدید با سرعت N ˙ در واحد حجم پیش خواهد رفت، که با سرعت رشد G ˙ به ذرات کروی تبدیل می شوند و تنها زمانی رشد نمی کنند که به یکدیگر برخورد کنند. در یک بازه زمانی 0 < τ < t ، هسته زایی و رشد فقط می تواند در مواد تبدیل نشده اتفاق بیفتد. با این حال، با این مشکل به کارگیری مفهوم یک حجم توسعه یافته - حجم فاز جدیدی که ایجاد می شد اگر کل نمونه هنوز تبدیل نشده باشد، قابل حل است. در طول بازه زمانی τ تا τ + d τ تعداد هسته های N که در نمونه ای از حجم V ظاهر و ایجاد می شوند توسط معادله زیر داده می شود: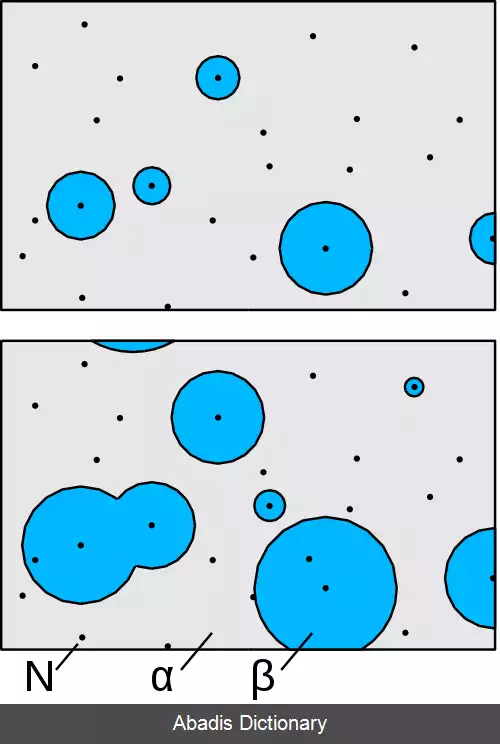
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین معادله با نام معادله جانسون – مهل – اورامی – کلموگروف ( JMAK ) نیز شناخته می شود. این معادله برای اولین بار توسط جانسون، مهل، اورامی و کولموگروف ( به زبان روسی ) در مجموعه ای از مقالات منتشر شده در مجله فیزیک شیمی بین سال های 1939 و 1941 استخراج شده است. [ ۲] [ ۳] [ ۴] علاوه بر این، کولموگروف از نظر آماری تبلور یک جامد را در سال 1937 بررسی کرد ( به روسی، Kolmogorov، AN، Izv. آکاد. ناوک. SSSR. , 1937, 3, 355 ) .
تغییرات اغلب یک روند s شکل یا سیگموئیدی را طی می کنند که در آن نرخ تبدیل در ابتدا و انتهای تبدیل کم است، اما در بین آن ها سریع است.
سرعت آهسته در مراحل اول را می توان به زمان مورد نیاز برای تشکیل و شروع رشد تعداد قابل توجهی از هسته های فاز جدید نسبت داد. در طول دوره میانی، سرعت تبدیل سریع است زیرا هسته ها به ذرات تبدیل می شوند و فاز قدیمی را مصرف می کنند در حالی که هسته ها در فاز اصلی باقی مانده به شکل گیری ادامه می دهند.
هنگامی که تبدیل به مراحل نهایی نزدیک می شود، مواد تغییر نیافته کمی برای هسته سازی بیشتر باقی می ماند و تولید ذرات جدید شروع به کند شدن می کند. علاوه بر این، ذرات تشکیل شده قبلی شروع به تماس با یکدیگر می کنند و مرزی را تشکیل می دهند که در آن رشد متوقف می شود.
برای استخراج ساده ترین حالت معادله آورامی تعداد قابل توجهی فرض و ساده سازی را ایجاد می کند: [ ۵]
• هسته زایی به طور تصادفی و همگن در کل بخش تبدیل نشده ماده رخ می دهد.
• نرخ رشد به میزان استحاله فازی بستگی ندارد.
• رشد در همه جهات با سرعت یکسان اتفاق می افتد.
اگر این شرایط برآورده شود، تغییر فاز α به β با هسته زایی ذرات جدید با سرعت N ˙ در واحد حجم پیش خواهد رفت، که با سرعت رشد G ˙ به ذرات کروی تبدیل می شوند و تنها زمانی رشد نمی کنند که به یکدیگر برخورد کنند. در یک بازه زمانی 0 < τ < t ، هسته زایی و رشد فقط می تواند در مواد تبدیل نشده اتفاق بیفتد. با این حال، با این مشکل به کارگیری مفهوم یک حجم توسعه یافته - حجم فاز جدیدی که ایجاد می شد اگر کل نمونه هنوز تبدیل نشده باشد، قابل حل است. در طول بازه زمانی τ تا τ + d τ تعداد هسته های N که در نمونه ای از حجم V ظاهر و ایجاد می شوند توسط معادله زیر داده می شود:


wiki: معادله آورامی
