معادله فریس یا فرمول فریس، به نام مهندس برق دانمارکی - آمریکایی هارالد تی فریس نامگذاری شده است، هر دو معادله مورد استفاده در مهندسی مخابرات برای محاسبه نسبت سیگنال به نویز یک تقویت کننده چند طبقه است. یکی مربوط به ضریب نویز است در حالی که دیگری مربوط به دمای نویز است.
معادله فریس برای محاسبه ضریب نویز کلی آبشاری از طبقات استفاده می شود، هر یک با ضریب نویز و بهره توان خود ( با فرض تطبیق امپدانس ها در هر طبقه ) . سپس می توان از ضریب نویز کل برای محاسبه عدد نویز کلی استفاده کرد. ضریب نویز کل داده می شود به صورت
F total = F 1 + F 2 − 1 G 1 + F 3 − 1 G 1 G 2 + F 4 − 1 G 1 G 2 G 3 + ⋯ + F n − 1 G 1 G 2 ⋯ G n − 1
که F i و G i ضریب نویز و بهره توان موجود به ترتیب از طبقه i ام هستند و n تعداد طبقه است. هر دو اندازه به صورت نسبت بیان می شوند نه به دسی بل.
معادله فریس را می توان با توجه به دمای نویز بیان کرد:
T eq = T 1 + T 2 G 1 + T 3 G 1 G 2 + ⋯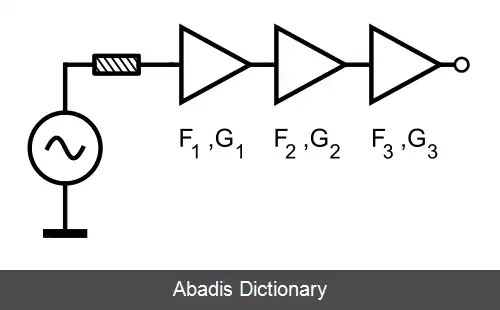
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمعادله فریس برای محاسبه ضریب نویز کلی آبشاری از طبقات استفاده می شود، هر یک با ضریب نویز و بهره توان خود ( با فرض تطبیق امپدانس ها در هر طبقه ) . سپس می توان از ضریب نویز کل برای محاسبه عدد نویز کلی استفاده کرد. ضریب نویز کل داده می شود به صورت
F total = F 1 + F 2 − 1 G 1 + F 3 − 1 G 1 G 2 + F 4 − 1 G 1 G 2 G 3 + ⋯ + F n − 1 G 1 G 2 ⋯ G n − 1
که F i و G i ضریب نویز و بهره توان موجود به ترتیب از طبقه i ام هستند و n تعداد طبقه است. هر دو اندازه به صورت نسبت بیان می شوند نه به دسی بل.
معادله فریس را می توان با توجه به دمای نویز بیان کرد:
T eq = T 1 + T 2 G 1 + T 3 G 1 G 2 + ⋯

wiki: معادلات فریس برای نویز
