معادلات تلگرافی یا معادلات تلگراف جفت معادله هایی زوج شده از نوع دیفرانسیل پاره ای هستند که رفتار خطوط انتقال مانند خطوط تلگراف، تلفن، مدارهای فرکانس بالا، خطوط انتقال برق و … را توصیف می کنند. این معادلات را نخستین بار الیور هویساید در سال ۱۸۸۰ به دست آورد.
برای به دست آوردن این معادلات، برای هر جز دیفرانسیلی از طول خط انتقال، یه مدل دوقطبی در نظر می گیریم. این مدل شامل اجزای زیر است:
• مقاومت سری R d x {\displaystyle Rdx} : هر محیط انتقالی در طول خود مقاومتی در مقابل جریان دارد که با این عنصر مدل می شود.
• اندوکتانس سری L d x {\displaystyle Ldx} : هر خط انتقال به علت داشتن میدان مغناطیسی، اندوکتانسی دارد.
• خازن موازی C d x {\displaystyle Cdx} : هر خط انتقال به علت داشتن میدان الکتریکی، ظرفیت خازنی دارد.
• رسانایی ( عکس مقاومت ) موازی G d x {\displaystyle Gdx} : خطوط انتقال علاوه بر مقاومت در طول خود در عرض خود نیز نوعی اتصال الکتریکی و در نتیجه مقاومت الکتریکی دارند.
معادلات تلگرافی رو می توان از اعمال قوانین کیرشهف در مدل دوقطبی به دست آمده استخراج کرد. به این منظور جریان ها و ولتاژها را دارای تابعیت زمانی و مکانی فرض می کنیم. جریان و ولتاژ ورودی را به صورت I ( x , t ) و V ( x , t ) در نظر می گیریم و جریان و ولتاژ خروجی را به صورت I ( x + Δ x , t ) و V ( x + Δ x , t ) فرض می کنیم. با به دست آوردن روابط و حدگیری از معادلات وقتی x به صفر میل کند، روابط زیر را به دست می آوریم:
از ترکیب این دو معادله، معادلات ی تلگرافی برای جریان و ولتاژ به دست می آیند:
این معادلات برای یک خط انتقال تلف دار است. در حالت ایده آل، برای یک خط انتقال بی اتلاف، مقدار عناصر R و G صفر است.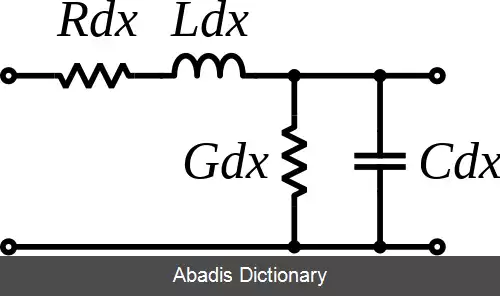
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای به دست آوردن این معادلات، برای هر جز دیفرانسیلی از طول خط انتقال، یه مدل دوقطبی در نظر می گیریم. این مدل شامل اجزای زیر است:
• مقاومت سری R d x {\displaystyle Rdx} : هر محیط انتقالی در طول خود مقاومتی در مقابل جریان دارد که با این عنصر مدل می شود.
• اندوکتانس سری L d x {\displaystyle Ldx} : هر خط انتقال به علت داشتن میدان مغناطیسی، اندوکتانسی دارد.
• خازن موازی C d x {\displaystyle Cdx} : هر خط انتقال به علت داشتن میدان الکتریکی، ظرفیت خازنی دارد.
• رسانایی ( عکس مقاومت ) موازی G d x {\displaystyle Gdx} : خطوط انتقال علاوه بر مقاومت در طول خود در عرض خود نیز نوعی اتصال الکتریکی و در نتیجه مقاومت الکتریکی دارند.
معادلات تلگرافی رو می توان از اعمال قوانین کیرشهف در مدل دوقطبی به دست آمده استخراج کرد. به این منظور جریان ها و ولتاژها را دارای تابعیت زمانی و مکانی فرض می کنیم. جریان و ولتاژ ورودی را به صورت I ( x , t ) و V ( x , t ) در نظر می گیریم و جریان و ولتاژ خروجی را به صورت I ( x + Δ x , t ) و V ( x + Δ x , t ) فرض می کنیم. با به دست آوردن روابط و حدگیری از معادلات وقتی x به صفر میل کند، روابط زیر را به دست می آوریم:
از ترکیب این دو معادله، معادلات ی تلگرافی برای جریان و ولتاژ به دست می آیند:
این معادلات برای یک خط انتقال تلف دار است. در حالت ایده آل، برای یک خط انتقال بی اتلاف، مقدار عناصر R و G صفر است.

wiki: معادلات تلگرافی
