مشتق گیری از تابع های مثلثاتی یک فرایند ریاضی است که برای یافتن مشتق یک تابع مثلثاتی یا نرخ تغییرات آن برحسب متغیر، انجام می شود. مشتق همه تابع های مثلثاتی را می توان برحسب مشتق سینوس و کسینوس به دست آورد. زیرا همه این تابع ها را می توان به صورت تابعی از سینوس یا کسینوس بیان کرد. قاعده خارج قسمت برای مشتق گیری از تابع مورد نظر به کار می رود. مشتق تابع های وارون مثلثاتی با استفاده از مشتق ضمنی و مشتق تابع های معمول مثلثاتی، قابل محاسبه است.
به طور خلاصه، مشتق تابع های مثلثاتی و مشتق تابع های وارون مثلثاتی را می توان در جدول زیر نشان داد:
برای اثبات مشتق ها نخست باید چند قضیه مهم حد که در استخراج رابطه برای مشتق ها مورد نیاز هستند، اثبات شوند.
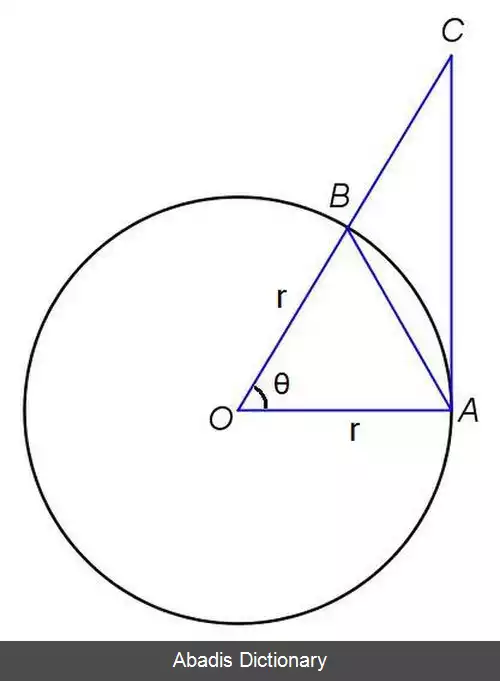
نمودار سمت چپ، یک دایره به مرکز O و شعاع r را نشان می دهد. زاویه θ در مرکز دایره قرار دارد و از دو شعاع OA و OB ساخته شده است. از آن جایی که می خواهیم θ را به سمت صفر میل دهیم، آن را یک مقدار کوچک مثبت در نظر می گیریم.
اکنون دو مثلث OAB و OAC و قطاع دایره ای OAB بین آن ها را در نظر می گیریم. از روی شکل به سادگی می توان گفت که نامعادله زیر بین مساحت این سه شکل برقرار است:
برپایه تابع های مثلثاتی، مساحت مثلث ها به دست می آید:
• مثلث OAB ( کوچک ) : ۱۲ ||OA||. ||OB|| . sinθ = ۱۲ r۲ . sinθ
• مثلث OAC ( بزرگ ) : ۱۲ ||OA||. ||AC|| = ۱۲ r. r. tanθ = ۱۲ r۲ . tanθ
مساحت قطاع OAB که روبرو به زاویه θ است، نیز برابر است با ۱۲ θr۲.
با جایگذاری مقادیر بالا در نامعادله، داریم:
از آن جایی که شعاع دایره بزرگتر از صفر است، می توان طرف های نامعادله را بر r۲ تقسیم کرد. هم چنین با توجه به این که زاویه θ بزرگ تر از صفر است، سینوس آن نیز بزرگ تر از صفر می باشد و می توان طرف های نامعادله را بر sinθ نیز تقسیم کرد؛ بنابراین، نامعادله به صورت زیر در می آید:
در نامعادله دوم خط بالا، طرف های نامعادله معکوس شدند و از آن جایی که هر سه طرف مثبت هستند، پس از معکوس کردن، علامت نامساوی نیز عکس می شود. اگر از این نامعادله را در نزدیکی صفر حد بگیریم:
• طرف سمت چپ نامعادله مقدار ثابت یک است.
• طرف راست نامعادله، cos ( θ ) است که با نزدیک شدن به صفر، مقدار آن به یک میل می کند.
اکنون با استفاده از قضیه فشردگی، می توان حد sin xx در x→۰ را به دست آورد. از آن جایی که این تابع بین دو تابع دیگر قرار دارد که حد هر دو در صفر، برابر یک است، پس حد این تابع نیز برابر با یک خواهد بود: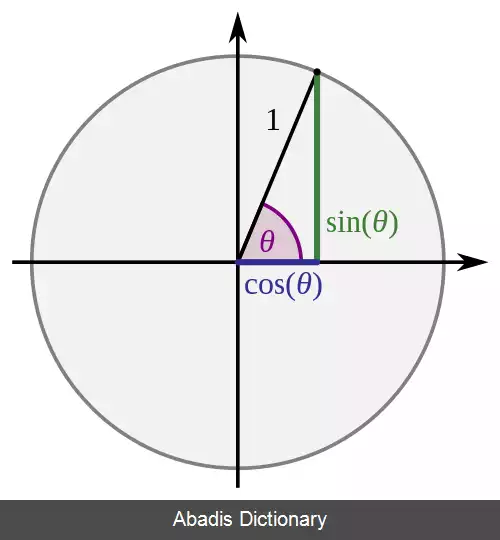
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه طور خلاصه، مشتق تابع های مثلثاتی و مشتق تابع های وارون مثلثاتی را می توان در جدول زیر نشان داد:
برای اثبات مشتق ها نخست باید چند قضیه مهم حد که در استخراج رابطه برای مشتق ها مورد نیاز هستند، اثبات شوند.
نمودار سمت چپ، یک دایره به مرکز O و شعاع r را نشان می دهد. زاویه θ در مرکز دایره قرار دارد و از دو شعاع OA و OB ساخته شده است. از آن جایی که می خواهیم θ را به سمت صفر میل دهیم، آن را یک مقدار کوچک مثبت در نظر می گیریم.
اکنون دو مثلث OAB و OAC و قطاع دایره ای OAB بین آن ها را در نظر می گیریم. از روی شکل به سادگی می توان گفت که نامعادله زیر بین مساحت این سه شکل برقرار است:
برپایه تابع های مثلثاتی، مساحت مثلث ها به دست می آید:
• مثلث OAB ( کوچک ) : ۱۲ ||OA||. ||OB|| . sinθ = ۱۲ r۲ . sinθ
• مثلث OAC ( بزرگ ) : ۱۲ ||OA||. ||AC|| = ۱۲ r. r. tanθ = ۱۲ r۲ . tanθ
مساحت قطاع OAB که روبرو به زاویه θ است، نیز برابر است با ۱۲ θr۲.
با جایگذاری مقادیر بالا در نامعادله، داریم:
از آن جایی که شعاع دایره بزرگتر از صفر است، می توان طرف های نامعادله را بر r۲ تقسیم کرد. هم چنین با توجه به این که زاویه θ بزرگ تر از صفر است، سینوس آن نیز بزرگ تر از صفر می باشد و می توان طرف های نامعادله را بر sinθ نیز تقسیم کرد؛ بنابراین، نامعادله به صورت زیر در می آید:
در نامعادله دوم خط بالا، طرف های نامعادله معکوس شدند و از آن جایی که هر سه طرف مثبت هستند، پس از معکوس کردن، علامت نامساوی نیز عکس می شود. اگر از این نامعادله را در نزدیکی صفر حد بگیریم:
• طرف سمت چپ نامعادله مقدار ثابت یک است.
• طرف راست نامعادله، cos ( θ ) است که با نزدیک شدن به صفر، مقدار آن به یک میل می کند.
اکنون با استفاده از قضیه فشردگی، می توان حد sin xx در x→۰ را به دست آورد. از آن جایی که این تابع بین دو تابع دیگر قرار دارد که حد هر دو در صفر، برابر یک است، پس حد این تابع نیز برابر با یک خواهد بود:


wiki: مشتق توابع مثلثاتی
