در نظریه گراف، مسیر همیلتونی ( به انگلیسی: Hamilton path ) مسیری در یک گراف ساده است که هر راس را دقیقاً یک بار مشاهده می کند. مدار همیلتونی ( یا دور همیلتونی ) مداری در یک گراف جهت دار است که دقیقاً یک بار هر رأس را مشاهده کرده و همچنین به رأس آغازین بر می گردد. در این گراف بر خلاف گراف اویلری نیازی نیست که از همه یال ها عبور کنیم. مسیر و مدار همیلتونی به نام ویلیام رومن همیلتون[ ۱] نام گذاری شده اند. ویلیام همیلتون بازی ایکوسیان را که امروزه به نام پازل همیلتون معروف است اختراع کرد. این بازی شامل یافتن یک مدار همیلتونی در گراف یالی یک دوازده سطحی است. با وجود اینکه دور همیلتونی به اسم ویلیام همیلتون نامگذاری شده است، دورهای همیلتونی در چندضلعی ها حدود یک سال پیش توسط توماس کرکمن مورد بررسی قرار گرفته بود، وی به طور اخص نمونه ای از یک چند ضلعی بدون دور همیلتونی را ارائه داده بود. [ ۲] حتی قبل از آن، دورها و مسیرهای همیلتونی در مسئله گراف اسب در شطرنج، که به سفر اسب ها نیز شهرت دارد در قرن نهم میلادی توسط روداتا، ریاضی دان هندی و العدلی الرومی، ریاضی دان مسلمان مورد مطالعه قرار گرفته بود. در قرن هجدهم مسئله سفر اسب ها توسط لئونارد اویلر و ابراهام دو مواور منتشر شد. [ ۳]
یک مسیر همیلتونی یا مسیر قابل تعقیب، مسیری است که هر راس را دقیقاً یک بار مشاهده کند. گرافی را که دارای مسیر همیلتونی باشد، گراف قابل تعقیب یا نیمه همیلتونی می نامند. هم چنین گرافی همیلتون - متصل است اگر برای هر زوج از رئوس آن، مسیری همیلتونی بین آن دو راس وجود داشته باشد.
مدار همیلتونی یا دور همیلتونی، مداری است که هر راس را دقیقاً یک بار مشاهده می کند ( به جز راسی که هم به عنوان آغاز و هم پایان است در نتیجه این راس دو بار دیده می شود ) . به طور قراردادی، گرافی کوچک شامل یک گره، دارای مدار همیلتونی است، ولی گراف متصلی دارای دو گره، شامل مدار همیلتونی نیست.
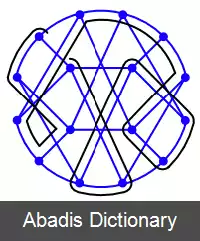
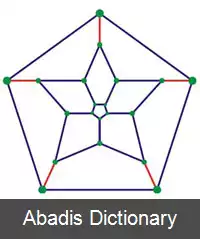
گرافی که دارای مدار همیلتونی باشد، گراف همیلتونی نامیده می شود. هر گراف کامل که بیشتر از دو راس داشته باشد، همیلتونی است. گرافی با نام گراف همیلتون وجود دارد که یک دوازده وجهی منتظم است و دارای دورهای همیلتونی زیبا است. ( شکل ( ۳ ) )
مسئله فروشنده دوره گرد برای دانشمندانی که روی مسائل NP کار می کنند، بسیار آشنا است. صورت این مسئله به این گونه است که فرض کنید فروشنده دوره گردی داریم که می خواهد برای فروش کالاهای خود، به چند شهر سفر کند. فرض کنید بین این چند شهر راه های مختلفی با طول مسیرهای مختلفی وجود دارد. حال این فروشنده دوره گرد از چه راه هایی برود تا همه شهرها را یکبار بپیماید و در کوتاه ترین مسیر حرکت کرده و در کمترین زمان به شهر اولی که از آن شروع کرده بود برسد. این مسئله ابتدا به صورت ریاضی مدل می شود و تبدیل به مسئله مدار همیلتونی در علم ریاضی و نظریه گراف ها می شود و سپس برای حل آماده می گردد. بسیاری از دانشمندان برای حل مسائل NP بیشتر روی مسئله فروشنده دوره گرد کار می کنند. تعیین شرط یا شروط لازم و کافی برای وجود داشتن مسیر یا دور همیلتونی در یک گراف هنوز به عنوان یک مسئله لاینحل باقی مانده است، ولی شروط لازم خوبی وجود دارند که به صورت قضیه مطرح شده اند. همچنین الگوریتمی احتمالی که توسط آقای ویلف ( ۱۹۹۴ ) شرح داده شده است، می تواند برای یافتن مسیر و مدار همیلتونی مفید باشد.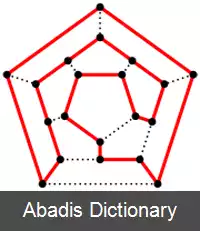
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک مسیر همیلتونی یا مسیر قابل تعقیب، مسیری است که هر راس را دقیقاً یک بار مشاهده کند. گرافی را که دارای مسیر همیلتونی باشد، گراف قابل تعقیب یا نیمه همیلتونی می نامند. هم چنین گرافی همیلتون - متصل است اگر برای هر زوج از رئوس آن، مسیری همیلتونی بین آن دو راس وجود داشته باشد.
مدار همیلتونی یا دور همیلتونی، مداری است که هر راس را دقیقاً یک بار مشاهده می کند ( به جز راسی که هم به عنوان آغاز و هم پایان است در نتیجه این راس دو بار دیده می شود ) . به طور قراردادی، گرافی کوچک شامل یک گره، دارای مدار همیلتونی است، ولی گراف متصلی دارای دو گره، شامل مدار همیلتونی نیست.
گرافی که دارای مدار همیلتونی باشد، گراف همیلتونی نامیده می شود. هر گراف کامل که بیشتر از دو راس داشته باشد، همیلتونی است. گرافی با نام گراف همیلتون وجود دارد که یک دوازده وجهی منتظم است و دارای دورهای همیلتونی زیبا است. ( شکل ( ۳ ) )
مسئله فروشنده دوره گرد برای دانشمندانی که روی مسائل NP کار می کنند، بسیار آشنا است. صورت این مسئله به این گونه است که فرض کنید فروشنده دوره گردی داریم که می خواهد برای فروش کالاهای خود، به چند شهر سفر کند. فرض کنید بین این چند شهر راه های مختلفی با طول مسیرهای مختلفی وجود دارد. حال این فروشنده دوره گرد از چه راه هایی برود تا همه شهرها را یکبار بپیماید و در کوتاه ترین مسیر حرکت کرده و در کمترین زمان به شهر اولی که از آن شروع کرده بود برسد. این مسئله ابتدا به صورت ریاضی مدل می شود و تبدیل به مسئله مدار همیلتونی در علم ریاضی و نظریه گراف ها می شود و سپس برای حل آماده می گردد. بسیاری از دانشمندان برای حل مسائل NP بیشتر روی مسئله فروشنده دوره گرد کار می کنند. تعیین شرط یا شروط لازم و کافی برای وجود داشتن مسیر یا دور همیلتونی در یک گراف هنوز به عنوان یک مسئله لاینحل باقی مانده است، ولی شروط لازم خوبی وجود دارند که به صورت قضیه مطرح شده اند. همچنین الگوریتمی احتمالی که توسط آقای ویلف ( ۱۹۹۴ ) شرح داده شده است، می تواند برای یافتن مسیر و مدار همیلتونی مفید باشد.



wiki: مسیر همیلتونی
