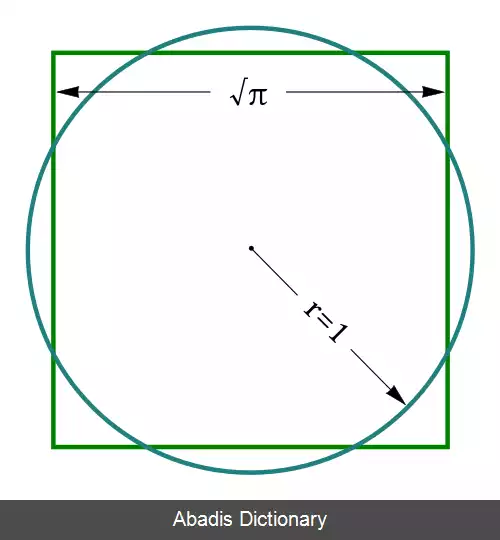
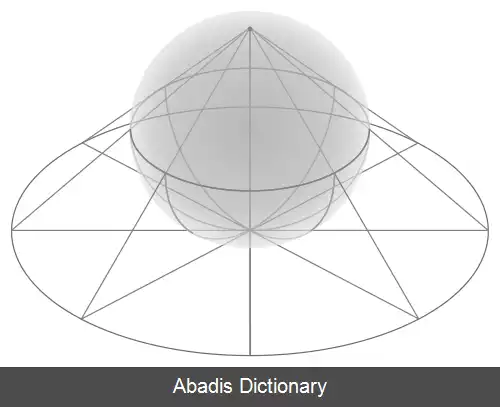
مساحت. [ م َ ح َ ] ( ع مص ) مساحة. زمین پیمودن. ( تاج المصادر بیهقی ) . پیمودن زمین. زمین پیمایی. پیمایش. و رجوع به مساحة شود. || ( اِ ) سطح قسمتی معین از محوطه ای : مساحت مثلث ، مساحت مربع، مساحت دایره :
... [مشاهده متن کامل]
که دانست چندین زمین با مساحت
صد و شصت بار است خورشید تابان.
ناصرخسرو.
به ساحت مساحت ملکوت او نرسد. ( سندبادنامه ص 2 ) .
مساحة. [ م ِ ح َ ] ( ع مص ، اِ ) مساحه. مساحت. پیمودن زمین. ( منتهی الارب ) . زمین پیمودن. ( المصادر زوزنی ) ( تاج المصادر بیهقی ) ( دهار ) . ذرع کردن زمین. ( اقرب الموارد ) . و رجوع به مساحت شود. || تقسیم کردن زمین با مقیاس و تخمین قیمت و ارزش آن. ( اقرب الموارد ) .
- علم مساحة؛ علمی است که از مقادیر خطوط و سطحها و اجسام ، و تعیین خط و مربع و مکعب بحث می کند، و در امر خراج و تقسیم اراضی و تخمین مساکن ارزشی فراوان دارد. ( اقرب الموارد ) ( از کشاف اصطلاحات الفنون ) .
منبع. لغت نامه دهخدا
منبع. عکس فرهنگ ریشه واژگان فارسی دکتر علی نورایی
واژه ی مساحت خود پهلوی است و از دو بخش
مسای یاد تشکیل شد و پسوند یاد مثل داد در بغداد و یاد در بنیاد است که به عربی رفته و ایة شده مثل بنیه از بنیت و از بنیاد
مسایاد>>مساحت
Masai ( پهلوی ) اندازه پهنا و ارتفاع. به اندازه ی
... [مشاهده متن کامل]
مثل pahlu masai بدرازای یک دنده
Sinak masai به حجم یک سینه
Tan mesai به اندازه یک نفر
یه مسلمون نیومد بگه مساحت به انگلیسی چی میشه!! خسته نباشید واقعا، میشه area دوستانی که قاعدتا برای همین ترثرجمه انگلیسی دنبالشین
میتوان از واژه یِ {دَردیسه} به جایِ {مساحت} و {بَردیسه} به جایِ {محیط} بکار برد.
{دَردیسه} از پیشوندِ {دَر:درون، اندر، در} به همراهِ {دیسه:شکل} و {بَردیسه} از پیشوندِ {بَر:کنار، دور و بر} به همراهِ {دیسه:شکل} ساخته شده است.
بِدرود!
پهنه، برابر این واژه است.
درود بر کاربر گرامی /آریا گل پرور/. پیشنهاد نخستین شما "گسترا"، شوربختانه درست نیست ولی واژه سازی خوبی انجام دادید.
گسترا از دو بخش گستر - ا درست شده است، که خب گستر بن کنونی گستردن است و پسوند "ا"، پسوند کنشگر ( =فاعل ) ساز است به این گونه که واژه ای می سازد که کننده بن واژه ( =مصدر ) ش است. برای نمونه کوشا از کوشیدن می آید که خب بر پایه چیزی که گفتیم، می شود چیزی که کوشیدن را انجام می دهد. این پسوند برابر پسوند های "نده، گر، کار" است.
... [مشاهده متن کامل]
پس گسترا می شود چیزی که گستردن را انجام می دهد، یا گسترش دهنده که برابر مساحت نیست.
ولی شما واژه سازی های خوبی را انجام دادید و جای آفرین گفتن دارد!
مساحت: همتای پارسی این واژه ی عربی، این است:
فنساخ fansāx ( سغدی )
واژه مساحت
معادل ابجد 509
تعداد حروف 5
تلفظ masāhat
نقش دستوری اسم
ترکیب ( اسم مصدر ) [عربی: مِساحة]
مختصات ( مِ حَ ) [ ع . مساحة ] ( مص م . )
آواشناسی masAhat
الگوی تکیه WWS
... [مشاهده متن کامل]
شمارگان هجا 3
منبع لغت نامه دهخدا
فرهنگ فارسی عمید
فرهنگ فارسی معین
فرهنگ واژه های سره
فرهنگ فارسی هوشیار
پهنه
گسترا
نمونه:
Th —> ث یا ز
زِم —> تم ( them )
——— از این نگر
ارد - ارت - ارث - ارده - ارته - ارثه
Erde - aarde - eorthe - —> Earth
ارز ~ ارت - ارزه ~ ارته - ارزا ~ ارتا
ارز ( ارض، گستره، مساحت )
ارزه ( پهنه، عرصه )
ارزا ( زِم گَرد~ گردنده بر زمین، مساح )
گستره
مقدار سطح محصور یک شکل — دایره، مثلث ، . . .
سطح دایره - سطح مثلث
دقیقا به گستردگی یک محدوده مربوط میشود، پس:
گستره دایره و گستره مثلث و . . .
اندازه
نوشتم نظر
من نمیدونم معنی مساحت چیست و زدم تو گوگل
من میدونم معنی مساحت درست است یا نه
فکر کنم درست باشه
این واژه سریانی است // مشوحتا //
پوشینه، پوشانه، رویه، پهنگی، رویگی، روسنج
متراژ
مقدار گسترش مکانی
وسعت
مشاهده ادامه پیشنهادها (١٠ از ٢٠)