۱۰۰ عدد زندانی موجودند که شماره های ۱ تا ۱۰۰ دارند و ۱۰۰ تا کشو وجود دارد که درون هر کدام یکی از اعداد ۱ تا ۱۰۰ وجود دارد هر زندانی می تواند بدون اینکه با دیگر زندانی ها صحبت کند ۵۰ تا از این کشوها را باز کند. در صورتی جان سالم به در می برند که همه زندانی ها شماره های خود را پیدا کرده باشند ( اگر حتی یک نفر شماره خود را پیدا نکند همه زندانی خواهند ماند ) . دانشمندی دانمارکی به نام پیتر برو میلترسون برای اولین بار در سال ۲۰۰۳ استراتژی ای برای این مسئله ارائه کردند که شانس خوبی برای نجات یافتن همهٔ زندانی ها باشد.
اگر یک زندانی ۵۰ کشو را با هم به صورت رندوم انتخاب کند به احتمال ۵۰٪ عددش در ۵۰ کشویی است که انتخاب کرده در نتیجه احتمال اینکه همه نجات یابند برابر است با:
( ½ ) 100 ≈ 0. 0000000000000000000000000000008
در این استراتژی ما ۵۰ کشو را با هم انتخاب نمی کنیم و از اطلاعات ای که با باز کردن کشو به دست می آوریم استفاده می کنیم. اول کشوها را به ترتیب ۱ تا ۱۰۰ شماره گذاری می کنیم. سپس زندانی شمارهٔ i ام کشوی شمارهٔ i ام را اول باز می کند اگر عدد درون آن i بود پس او نجات یافته است. اگر نه کشوای که شمارهٔ ان برابر با شمارهٔ درون کشو است را باز می کنیم. این عملیات را تا زمانی که ۵۰ کشو را انتخاب کرده باشید ادامه می دهد اگر در حین عملیات به i برسد زندانی نجات می یابد.
فرض کنید اعداد درون کشوها این گونه باشند:
در استراتژی ما هر زندانی این کارها را انجام می دهد:
• زندانی ۱ کشو ی شمارهٔ ۱ را باز می کند بعد در ان ۷ را می بیند. بعد کشو ی شمارهٔ ۷ را باز می کند بعد در ان ۵ را می بیند. بعد کشو ی شمارهٔ ۵ را باز می کند بعد در ان شمارهٔ خود را می بیند و نجات می یابد.
• زندانی ۲ کشو ی شمارهٔ ۲ و ۴و ۸ را باز می کند بعد در ۸ شمارهٔ خود را می بیند و نجات می یابد.
• زندانی ۳ کشو ی شمارهٔ ۳ و ۶ را باز می کند بعد در ۶ شمارهٔ خود را می بیند و نجات می یابد.
• زندانی ۴ کشو ی شمارهٔ ۴ و ۸و ۲ را باز می کند بعد در ۲ شمارهٔ خود را می بیند و نجات می یابد.
• همینگونه زندانی های ۵ تا هم شمارهٔ خود را پیدا می کنند.
در مثال بالا همه شمارهٔ خود را پیدا کردند اما همیشه اینطور نیست مثلاً فرض کنید اعداد درون کشوها این گونه باشد:
در این مثال زندانی اول کشوهای ۱ و ۳ و ۷ و۴ را باز می کند اما شمارهٔ خود را در آن پیدا نمی کند اما زندانی ۶ شمارهٔ خود را در اولین کشویی که باز می کند پیدا می کند.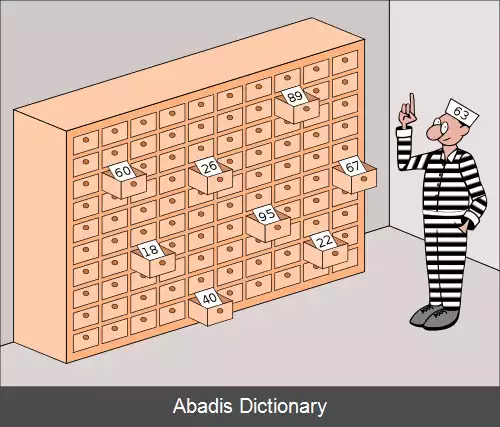
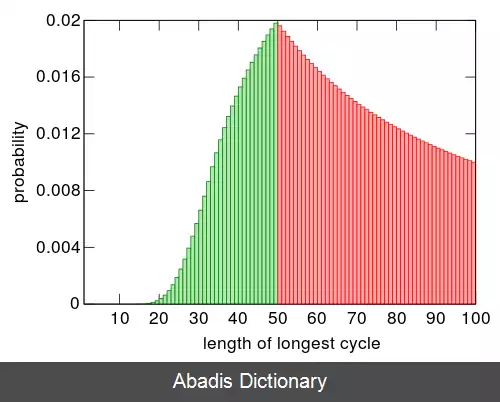
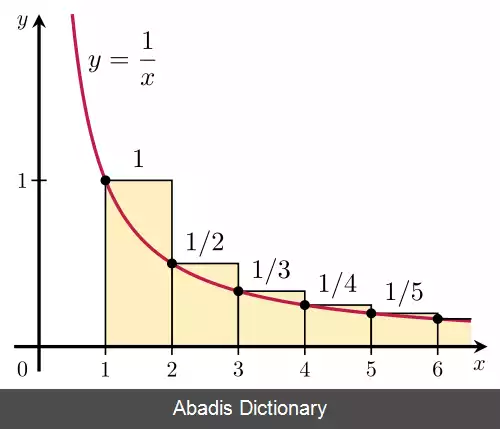
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر یک زندانی ۵۰ کشو را با هم به صورت رندوم انتخاب کند به احتمال ۵۰٪ عددش در ۵۰ کشویی است که انتخاب کرده در نتیجه احتمال اینکه همه نجات یابند برابر است با:
( ½ ) 100 ≈ 0. 0000000000000000000000000000008
در این استراتژی ما ۵۰ کشو را با هم انتخاب نمی کنیم و از اطلاعات ای که با باز کردن کشو به دست می آوریم استفاده می کنیم. اول کشوها را به ترتیب ۱ تا ۱۰۰ شماره گذاری می کنیم. سپس زندانی شمارهٔ i ام کشوی شمارهٔ i ام را اول باز می کند اگر عدد درون آن i بود پس او نجات یافته است. اگر نه کشوای که شمارهٔ ان برابر با شمارهٔ درون کشو است را باز می کنیم. این عملیات را تا زمانی که ۵۰ کشو را انتخاب کرده باشید ادامه می دهد اگر در حین عملیات به i برسد زندانی نجات می یابد.
فرض کنید اعداد درون کشوها این گونه باشند:
در استراتژی ما هر زندانی این کارها را انجام می دهد:
• زندانی ۱ کشو ی شمارهٔ ۱ را باز می کند بعد در ان ۷ را می بیند. بعد کشو ی شمارهٔ ۷ را باز می کند بعد در ان ۵ را می بیند. بعد کشو ی شمارهٔ ۵ را باز می کند بعد در ان شمارهٔ خود را می بیند و نجات می یابد.
• زندانی ۲ کشو ی شمارهٔ ۲ و ۴و ۸ را باز می کند بعد در ۸ شمارهٔ خود را می بیند و نجات می یابد.
• زندانی ۳ کشو ی شمارهٔ ۳ و ۶ را باز می کند بعد در ۶ شمارهٔ خود را می بیند و نجات می یابد.
• زندانی ۴ کشو ی شمارهٔ ۴ و ۸و ۲ را باز می کند بعد در ۲ شمارهٔ خود را می بیند و نجات می یابد.
• همینگونه زندانی های ۵ تا هم شمارهٔ خود را پیدا می کنند.
در مثال بالا همه شمارهٔ خود را پیدا کردند اما همیشه اینطور نیست مثلاً فرض کنید اعداد درون کشوها این گونه باشد:
در این مثال زندانی اول کشوهای ۱ و ۳ و ۷ و۴ را باز می کند اما شمارهٔ خود را در آن پیدا نمی کند اما زندانی ۶ شمارهٔ خود را در اولین کشویی که باز می کند پیدا می کند.



wiki: مسئله ۱۰۰ زندانی
