مسئله کم هزینه ترین جریان، پیدا کردن کم هزینه ترین راه فرستادن میزان مشخصی از جریان درون یک شبکه شاره است. حل این مسئله در زندگی روزمره کاربردهایی دارد از جمله شبکه های هزینه دار ( مانند شبکه های مخابراتی ) و هم چنین در مواردی که تناسب آن با مسئله خیلی مشهود نیست، مانند تعیین محل قرارگیری انبارها.
یک شبکه شاره داریم که آن را با گراف جهت دار G = ( V , E ) با مبدا s ∈ V و مقصد t ∈ V که در آن یال ( u , v ) ∈ E دارای ظرفیت c ( u , v ) > 0 ، جریان f ( u , v ) ≥ 0 و هزینه a ( u , v ) می باشد، نشان می دهیم ( اکثر الگوریتم های کم هزینه ترین جریان یال با هزینه منفی را پشتیبانی می کنند. ) هزینه فرستادن این جریان f ( u , v ) ⋅ a ( u , v ) است. شما باید جریان d را از s به t بفرستید.
تعریف مسئله کمینه کردن هزینه کل جریان است:
با شرط های زیر:
حالت دیگری از این مسئله پیدا کردن جریان بیشینه ای است که بین جریان های بیشینه کم ترین هزینه را دارد که می توان آن را مسئله کم هزینه ترین بیشینه جریان نامید. این حالت در پیدا کردن کم هزینه ترین تطابق بیشینه کاربرد دارد.
در بعضی راه حل ها پیدا کردن کم هزینه ترین بیشینه جریان ساده است. در غیر این صورت، می توان از جستجوی دودویی روی d استفاده کرد.
می توان از مسئله کم هزینه ترین گردش در حل این مسئله استفاده کرد. این کار با صفر قرار دادن کران پایین همه ی یال ها، اضافه کردن یک یال از مقصد t به مبدا s با ظرفیت c ( t , s ) = d و کران پایین l ( t , s ) = d و قرار دادن کل جریان برابر d انجام می شود.
دو مسئله زیر حالات خاص این مسئله به شمار می آیند:
• اگر محدودیت ظرفیت برداشته شود، به مسئله یافتن کوتاه ترین مسیر تبدیل می شود.
• اگر همه هزینه ها صفر باشند، به مسئله بیشینه جریان تبدیل می شود.
از آنجایی که ما تابعی خطی را بهینه میکنیم و تمام شروط خطی اند، این مسئله با استفاده از برنامه ریزی خطی قابل حل است.
علاوه بر آن الگوریتم های ترکیبیاتی مختلفی نیز وجود دارند، برای بررسی جامع تر، را ببینید. تعدادی از آن ها تعمیم الگوریتم بیشینه جریان هستند، بقیه روش های کاملاً متفاوتی استفاده میکنند.
الگوریتم های اساسی شناخته شده ( حالت های زیادی دارند ) :
• Cycle canceling یک روش کلی اولیه
• Minimum mean cycle canceling یک الگوریتم ساده قویا چندجمله ای
• Successive shortest path and capacity scaling روش های دوگانه که می توان آن ها را به عنوان تعمیم های الگوریتم فورد–فالکرسون در نظر گرفت.
• Cost scaling یک روش اولیه - دوگانه، که حالت کلی الگوریتم ارسال - برچسب است.
• Network simplex حالت خاص برنامه ریزی خطی غیر مرکب است که در زمان چندجمله ای اجرا می شود.
• الگوریتم Out - of - kilter توسط D. R. Fulkerson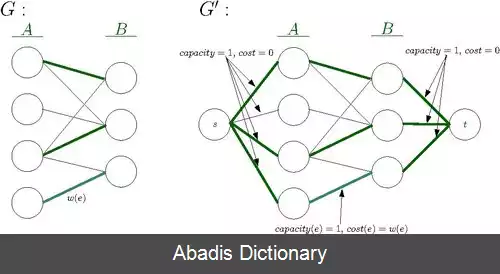
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک شبکه شاره داریم که آن را با گراف جهت دار G = ( V , E ) با مبدا s ∈ V و مقصد t ∈ V که در آن یال ( u , v ) ∈ E دارای ظرفیت c ( u , v ) > 0 ، جریان f ( u , v ) ≥ 0 و هزینه a ( u , v ) می باشد، نشان می دهیم ( اکثر الگوریتم های کم هزینه ترین جریان یال با هزینه منفی را پشتیبانی می کنند. ) هزینه فرستادن این جریان f ( u , v ) ⋅ a ( u , v ) است. شما باید جریان d را از s به t بفرستید.
تعریف مسئله کمینه کردن هزینه کل جریان است:
با شرط های زیر:
حالت دیگری از این مسئله پیدا کردن جریان بیشینه ای است که بین جریان های بیشینه کم ترین هزینه را دارد که می توان آن را مسئله کم هزینه ترین بیشینه جریان نامید. این حالت در پیدا کردن کم هزینه ترین تطابق بیشینه کاربرد دارد.
در بعضی راه حل ها پیدا کردن کم هزینه ترین بیشینه جریان ساده است. در غیر این صورت، می توان از جستجوی دودویی روی d استفاده کرد.
می توان از مسئله کم هزینه ترین گردش در حل این مسئله استفاده کرد. این کار با صفر قرار دادن کران پایین همه ی یال ها، اضافه کردن یک یال از مقصد t به مبدا s با ظرفیت c ( t , s ) = d و کران پایین l ( t , s ) = d و قرار دادن کل جریان برابر d انجام می شود.
دو مسئله زیر حالات خاص این مسئله به شمار می آیند:
• اگر محدودیت ظرفیت برداشته شود، به مسئله یافتن کوتاه ترین مسیر تبدیل می شود.
• اگر همه هزینه ها صفر باشند، به مسئله بیشینه جریان تبدیل می شود.
از آنجایی که ما تابعی خطی را بهینه میکنیم و تمام شروط خطی اند، این مسئله با استفاده از برنامه ریزی خطی قابل حل است.
علاوه بر آن الگوریتم های ترکیبیاتی مختلفی نیز وجود دارند، برای بررسی جامع تر، را ببینید. تعدادی از آن ها تعمیم الگوریتم بیشینه جریان هستند، بقیه روش های کاملاً متفاوتی استفاده میکنند.
الگوریتم های اساسی شناخته شده ( حالت های زیادی دارند ) :
• Cycle canceling یک روش کلی اولیه
• Minimum mean cycle canceling یک الگوریتم ساده قویا چندجمله ای
• Successive shortest path and capacity scaling روش های دوگانه که می توان آن ها را به عنوان تعمیم های الگوریتم فورد–فالکرسون در نظر گرفت.
• Cost scaling یک روش اولیه - دوگانه، که حالت کلی الگوریتم ارسال - برچسب است.
• Network simplex حالت خاص برنامه ریزی خطی غیر مرکب است که در زمان چندجمله ای اجرا می شود.
• الگوریتم Out - of - kilter توسط D. R. Fulkerson

