مسئلهٔ پایان خوش ( که توسط پل اردیش نامگذاری شده است، چرا که به ازدواج جورج سیکریس و استر کلاین منجر شد ) گزارهٔ ذیل است:
این قضیه یکی از نتایج اصلی است که منجر به ظهور نظریهٔ رمزی شد.
قضیهٔ پایان خوش، با تحلیل یک حالت ساده اثبات می شود: اگر چهار یا تعداد بیش تری نقطه، رأس های یک بدنهٔ محدب باشند، هر چهار نقطه ای به این شکل می توانند انتخاب شوند. از طرفی دیگر، اگر مجموعهٔ نقاط به فرم یک مثلث با دو نقطه درون آن باشند، دو نقطهٔ درونی و یکی از اضلاع مثلث می توانند انتخاب شوند. برای توضیح مصور این اثبات، پترسون ( ۲۰۰۰ ) را ببینید و برای بررسی دقیق تر این مسئله نسبت به آنچه اینجا ارائه شده است، موریس و سالتن ( ۲۰۰۰ ) را ببینید.
تخمین اردوش - سیکریس رابطهٔ کلی بین تعداد نقاطی که در یک مجموعهٔ نقاط با موقعیت عمومی هستند و بزرگ ترین چندضلعی محدب آن را به طور دقیق بیان می کند. این مسئله اثبات نشده باقی می ماند، اما مرزهای دقیق کم تری شناخته شده است.
دو دانشمند به نام های اردوش و سیکریس این قضیه را به صورت زیر تعمیم داده اند:
اثبات قضیه اردیش–ژکرس در مقاله ای که قضیهٔ زیردنباله های یکنواخت در دنباله های عددی را اثبات می کند آمده است.
فرض کنید ( f ( N کمترین مقدار M را نشان دهد که برای هر مجموعه از M نقطه در موقعیت عمومی یک Nضلعی محدب وجود داشته باشد. داریم:
• f ( ۳ ) = ۳، بدیهی.
• f ( ۴ ) = ۵. [ ۲]
• f ( ۵ ) = ۹. [ ۳] مجموعه ای از هشت نقطه که پنج ضلعی محدب ندارند در شکل نشان داده شده است، که نشان می دهد f ( 5 ) > ۸ است. قسمت دشوارتر اثبات این است که نشان دهیم هر مجموعه از ۹ نقطه در وضعیت معمولی دارای رئوس یک پنج ضلعی محدب است.
• f ( ۶ ) = ۱۷. [ ۴]
• مقدار f برای اعداد بیشتر از ۶ نامعلوم است، اما با توجه به نتیجهٔ مقالهٔ اردوش - سیکریس ( ۱۹۳۵ ) می دانیم مقدار متناهی دارد.
بر مبنای مقادیر مشخص ( f ( N، یعنی برای N = ۳, ۴, ۵، اردوش و سیکریس در مقالهٔ اصلی خود رابطهٔ زیر را تخمین زدند: به ازای هر N ≥ ۳
بعدها این دو نفر با زدن مثال های خارجی دیگر ثابت کردند که:
اما بهترین کران بالا برای حالت هایی که N ≥ ۷ است، به صورت زیر است:[ ۶]
ممکن است سؤال پیش بیاید که آیا برای هر مجموعهٔ کافی از نقاط در موقعیت عمومی دارای یک چهارضلعی، پنج ضلعی و. . هست یا نه، به این معنی که نیاز به نقطه ورودی جدید نداشته باشد. راه حل اصلی مسئلهٔ پایان خوش را می توان طوری تطابق داد که نشان دهد به ازای هر پنج نقطه با وضعیت موقعیت عمومی در صفحه یک چهارضلعی محدب خالی وجود دارد، همان طور که در تصویر نشان داده شده، و به ازای هر ده نقطه با شرایط فوق یک پنج ضلعی محدب خالی وجود دارد. [ ۷] اگرچه مجموعه های بزرگ و دلخواهی از نقاط با موقعیت عمومی ممکن است وجود داشته باشند که هیچ هفت ضلعی خالی برای آن ها یافت نشود. [ ۸] برای مدت طولانی این سؤال که آیا شش ضلعی خالی وجود دارد یا نه، بدون پاسخ ماند، ولی نیکولاس ( ۲۰۰۷ ) و گرکن ( ۲۰۰۸ ) ثابت کردند که به ازای هر مجموعهٔ کافی از نقاط با موقعیت عمومی در صفحه یک شش ضلعی محدب خالی وجود دارد. به صورت خاص، گرکن نشان داد که تعداد نقاط مورد نیاز بیشتر از ( f ( ۹ نیست. ( f در بالا تعریف شده ) درحالیکه نیکولاس نشان داد این مقدار حداکثر به اندازهٔ ( f ( ۲۵ است. ( Valtr ( ۲۰۰۶ اثبات گرکن را ساده می کند و نشان می دهد که به نقاط بیشتری از ( f ( ۹، یعنی به اندازهٔ ( f ( ۱۵ که برابر ۳۰ نقطه می شود، نیاز داریم، چرا که یک مجموعه از ۲۹ نقطه در موقعیت عمومی در صفحه وجود دارد که برای آن شش ضلعی محدب خالی وجود ندارد. [ ۹]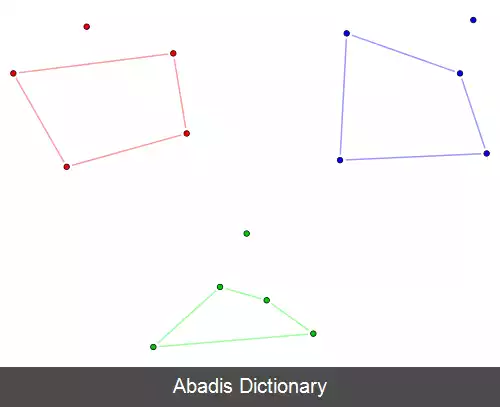

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین قضیه یکی از نتایج اصلی است که منجر به ظهور نظریهٔ رمزی شد.
قضیهٔ پایان خوش، با تحلیل یک حالت ساده اثبات می شود: اگر چهار یا تعداد بیش تری نقطه، رأس های یک بدنهٔ محدب باشند، هر چهار نقطه ای به این شکل می توانند انتخاب شوند. از طرفی دیگر، اگر مجموعهٔ نقاط به فرم یک مثلث با دو نقطه درون آن باشند، دو نقطهٔ درونی و یکی از اضلاع مثلث می توانند انتخاب شوند. برای توضیح مصور این اثبات، پترسون ( ۲۰۰۰ ) را ببینید و برای بررسی دقیق تر این مسئله نسبت به آنچه اینجا ارائه شده است، موریس و سالتن ( ۲۰۰۰ ) را ببینید.
تخمین اردوش - سیکریس رابطهٔ کلی بین تعداد نقاطی که در یک مجموعهٔ نقاط با موقعیت عمومی هستند و بزرگ ترین چندضلعی محدب آن را به طور دقیق بیان می کند. این مسئله اثبات نشده باقی می ماند، اما مرزهای دقیق کم تری شناخته شده است.
دو دانشمند به نام های اردوش و سیکریس این قضیه را به صورت زیر تعمیم داده اند:
اثبات قضیه اردیش–ژکرس در مقاله ای که قضیهٔ زیردنباله های یکنواخت در دنباله های عددی را اثبات می کند آمده است.
فرض کنید ( f ( N کمترین مقدار M را نشان دهد که برای هر مجموعه از M نقطه در موقعیت عمومی یک Nضلعی محدب وجود داشته باشد. داریم:
• f ( ۳ ) = ۳، بدیهی.
• f ( ۴ ) = ۵. [ ۲]
• f ( ۵ ) = ۹. [ ۳] مجموعه ای از هشت نقطه که پنج ضلعی محدب ندارند در شکل نشان داده شده است، که نشان می دهد f ( 5 ) > ۸ است. قسمت دشوارتر اثبات این است که نشان دهیم هر مجموعه از ۹ نقطه در وضعیت معمولی دارای رئوس یک پنج ضلعی محدب است.
• f ( ۶ ) = ۱۷. [ ۴]
• مقدار f برای اعداد بیشتر از ۶ نامعلوم است، اما با توجه به نتیجهٔ مقالهٔ اردوش - سیکریس ( ۱۹۳۵ ) می دانیم مقدار متناهی دارد.
بر مبنای مقادیر مشخص ( f ( N، یعنی برای N = ۳, ۴, ۵، اردوش و سیکریس در مقالهٔ اصلی خود رابطهٔ زیر را تخمین زدند: به ازای هر N ≥ ۳
بعدها این دو نفر با زدن مثال های خارجی دیگر ثابت کردند که:
اما بهترین کران بالا برای حالت هایی که N ≥ ۷ است، به صورت زیر است:[ ۶]
ممکن است سؤال پیش بیاید که آیا برای هر مجموعهٔ کافی از نقاط در موقعیت عمومی دارای یک چهارضلعی، پنج ضلعی و. . هست یا نه، به این معنی که نیاز به نقطه ورودی جدید نداشته باشد. راه حل اصلی مسئلهٔ پایان خوش را می توان طوری تطابق داد که نشان دهد به ازای هر پنج نقطه با وضعیت موقعیت عمومی در صفحه یک چهارضلعی محدب خالی وجود دارد، همان طور که در تصویر نشان داده شده، و به ازای هر ده نقطه با شرایط فوق یک پنج ضلعی محدب خالی وجود دارد. [ ۷] اگرچه مجموعه های بزرگ و دلخواهی از نقاط با موقعیت عمومی ممکن است وجود داشته باشند که هیچ هفت ضلعی خالی برای آن ها یافت نشود. [ ۸] برای مدت طولانی این سؤال که آیا شش ضلعی خالی وجود دارد یا نه، بدون پاسخ ماند، ولی نیکولاس ( ۲۰۰۷ ) و گرکن ( ۲۰۰۸ ) ثابت کردند که به ازای هر مجموعهٔ کافی از نقاط با موقعیت عمومی در صفحه یک شش ضلعی محدب خالی وجود دارد. به صورت خاص، گرکن نشان داد که تعداد نقاط مورد نیاز بیشتر از ( f ( ۹ نیست. ( f در بالا تعریف شده ) درحالیکه نیکولاس نشان داد این مقدار حداکثر به اندازهٔ ( f ( ۲۵ است. ( Valtr ( ۲۰۰۶ اثبات گرکن را ساده می کند و نشان می دهد که به نقاط بیشتری از ( f ( ۹، یعنی به اندازهٔ ( f ( ۱۵ که برابر ۳۰ نقطه می شود، نیاز داریم، چرا که یک مجموعه از ۲۹ نقطه در موقعیت عمومی در صفحه وجود دارد که برای آن شش ضلعی محدب خالی وجود ندارد. [ ۹]


wiki: مسئله پایان خوش
