مسئله کبریت باناخ یک مسئله کلاسیک در احتمال منسوب به استفن باناخ است.
فلر[ ۱] می گوید این مسئله با اشاره به شوخ طبعی به عادت سیگار کشیدن باناخ در سخنرانی بزرگداشت او توسط هوگو اشتاینهاوس الهام گرفته شده است، اما این باناخ نبود که این مسئله را تنظیم کرده یا پاسخی ارائه داده است.
فرض کنید یک ریاضیدان همیشه دو قوطی کبریت حمل می کند: یکی در جیب سمت چپ و دیگری در سمت راست. هر بار که به کبریت احتیاج داشت، به طور مساوی احتمال دارد آن را از هر جیبی بردارد. فرض کنید او دست در جیب خود کرده و برای اولین بار متوجه می شود که قوطی برداشته شده خالی است. اگر فرض شود که هر یک از جعبه های کبریت از اول شامل N کبریت است، چقدر احتمال دارد که در قوطی دیگر دقیقاً k کبریت وجود داشته باشد؟
بدون از دست دادن کلیت، موردی را در نظر بگیرید که در قوطی کبریت در جیب راست او تعداد نامحدودی کبریت وجود دارد و بگذارید M تعداد کبریت های حذف شده از این یکی باشد قبل از اینکه سمت چپی خالی شود. هنگامی که جیب سمت چپ خالی است، مرد آن جیب را ( N + 1 ) بار انتخاب کرده است؛ بنابراین M تعداد موفقیت ها قبل از ( N + 1 ) شکست در آزمایش ها برنولی با p = 1 / 2 است، که دارای توزیع دوجمله ای منفی است و بنابراین
با بازگشت به مسئله اصلی، می بینیم که احتمال این که ابتدا جیب سمت چپ خالی باشد P است که برابر 1 / 2 است، زیرا هر دو به یک اندازه محتمل هستند. ما می بینیم که تعداد K از کبریت های باقی مانده در جیب دیگر است:
چشم داشتی توزیع تقریباً 2 N / π − 1 است. ( این با استفاده از تقریب استرلینگ نشان داده شده است. [ ۲] ) بنابراین با قوطی هایی که با N = 40 کبریت شروع می شود، تعداد کبریت انتظاری در جعبه دوم برابر 6 است.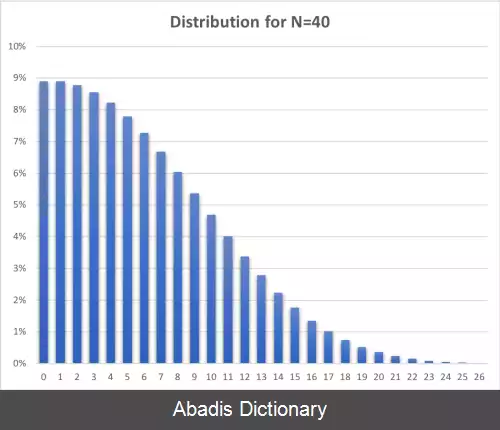
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففلر[ ۱] می گوید این مسئله با اشاره به شوخ طبعی به عادت سیگار کشیدن باناخ در سخنرانی بزرگداشت او توسط هوگو اشتاینهاوس الهام گرفته شده است، اما این باناخ نبود که این مسئله را تنظیم کرده یا پاسخی ارائه داده است.
فرض کنید یک ریاضیدان همیشه دو قوطی کبریت حمل می کند: یکی در جیب سمت چپ و دیگری در سمت راست. هر بار که به کبریت احتیاج داشت، به طور مساوی احتمال دارد آن را از هر جیبی بردارد. فرض کنید او دست در جیب خود کرده و برای اولین بار متوجه می شود که قوطی برداشته شده خالی است. اگر فرض شود که هر یک از جعبه های کبریت از اول شامل N کبریت است، چقدر احتمال دارد که در قوطی دیگر دقیقاً k کبریت وجود داشته باشد؟
بدون از دست دادن کلیت، موردی را در نظر بگیرید که در قوطی کبریت در جیب راست او تعداد نامحدودی کبریت وجود دارد و بگذارید M تعداد کبریت های حذف شده از این یکی باشد قبل از اینکه سمت چپی خالی شود. هنگامی که جیب سمت چپ خالی است، مرد آن جیب را ( N + 1 ) بار انتخاب کرده است؛ بنابراین M تعداد موفقیت ها قبل از ( N + 1 ) شکست در آزمایش ها برنولی با p = 1 / 2 است، که دارای توزیع دوجمله ای منفی است و بنابراین
با بازگشت به مسئله اصلی، می بینیم که احتمال این که ابتدا جیب سمت چپ خالی باشد P است که برابر 1 / 2 است، زیرا هر دو به یک اندازه محتمل هستند. ما می بینیم که تعداد K از کبریت های باقی مانده در جیب دیگر است:
چشم داشتی توزیع تقریباً 2 N / π − 1 است. ( این با استفاده از تقریب استرلینگ نشان داده شده است. [ ۲] ) بنابراین با قوطی هایی که با N = 40 کبریت شروع می شود، تعداد کبریت انتظاری در جعبه دوم برابر 6 است.

wiki: مسئله قوطی کبریت باناخ
