مسئله فرشته از مسائل نظریه بازی ها است که توسط هرتن کانوی پیشنهاد شد. این بازی معمولاً با نام فرشته ها شیاطین شناخته می شود. بازی دو بازیکن به نامهای فرشته و شیطان دارد و روی صفحهٔ شطرنج نا متناهی ( یا به طور هم ارز نقاط روی صفحه مشبّک دوبعدی ) بازی می شود. فرشته مانند شاه شطرنج حرکت می کند، امّا بسته به هر بازی قدرت متفاوتk ( عددی طبیعی بزرگتر یا مساوی ۱ ) دارد. بازی با صفحهٔ خالی و فرشته در خانهٔ شروع آغاز می شود. در هر نوبت فرشته به یک خانه متفاوت به فاصله حد اکثر k، یعنی خانه ای که با حد اکثر k حرکت فرشته قابل دسترسی است. ( فاصله از مربّع شروع در نرم نامتناهی حد اکثر kاست ) شیطان در هر نوبت می تواند مانعی در هر خانه به جز خانه حاوی فرشته قرار دهد. فرشته می تواند از روی موانع پرش کند، امّا نمی تواند در آن خانه ها قرار گیرد. در صورتی که فرشته قادر به انجام حرکتی نباشد، شیطان پیرّوز خواهد شد، همچنین اگر فرشته بتواند به تعداد نامتناهی بار نجات پیدا کند فرشته برنده خواهد بود.
باید استراتژی ای برای پیروزی یکی از دو بازیکن وجود داشته باشد. اگر شیطان برنده شود، این کار را در تعداد متناهی حرکت می تواند انجام دهد و اگر شیطان نتواند برنده شود، همواره حرکتی برای فرشته برای رهایی از شکست وجود خواهد داشت و استراتژی پیروزی برای او این خواهد بود که چنین حرکتی را انتخاب کند. به طور مطلق، مجموعه پرداخت ( مجموعه همه بازیهایی که در آن ها فرشته برنده می شود ) مجموعه ای بسته است، و این بازی ها مشخّص اند.
کانوی جایزی برای حل کلّی این مسئله ( ۱۰۰$ برای ارایهٔ یک استراتژی پیروزی برای فرشتی با قدرت کافی، و ۱۰۰۰$ برای اثبات این که شیطان می تواند مستقل از قدرت فرشته پیروز شود ) . ابتدا پیشرفتهایی در ابعاد بالاتر صورت گرفت و اثبات های زیبایی ارائه شد. در سال ۲۰۰۶، مسئله اصلی حل شد و ثابت شد که فرشته می تواند پیروز شود.
مسئله ابتدا در سال ۱۹۸۲ در کتاب استراتژی برد نوشته برلکمپ، کانوی و گای، با نام «فرشته و مربّع خوار» منتشر شد. در فضای دو بعدی. چند نتیجه جزئی شامل:
• اگر فرشته قدرت ۱ داشته باشد، شیطان استراتژی پیروزی دارد ( کانوی، ۱۹۸۲ ) ( طبق گفته کانوی این نتیجه گیری متعلق به برلکمپ است )
• اگر فرشته هرگز مولفه yخود را افزایش ندهد، شیطان استراتژی پیروزی دارد. ( کانوی ۱۹۸۲ )
• اگر فرشته همواره فصلهٔ خود را از مبدأ زیاد کند، شیطان استراتژی پیروزی دارد ( کانوی. ۱۹۹۶ )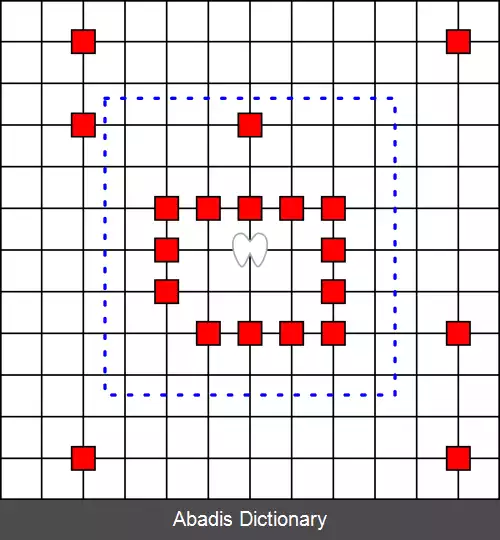
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفباید استراتژی ای برای پیروزی یکی از دو بازیکن وجود داشته باشد. اگر شیطان برنده شود، این کار را در تعداد متناهی حرکت می تواند انجام دهد و اگر شیطان نتواند برنده شود، همواره حرکتی برای فرشته برای رهایی از شکست وجود خواهد داشت و استراتژی پیروزی برای او این خواهد بود که چنین حرکتی را انتخاب کند. به طور مطلق، مجموعه پرداخت ( مجموعه همه بازیهایی که در آن ها فرشته برنده می شود ) مجموعه ای بسته است، و این بازی ها مشخّص اند.
کانوی جایزی برای حل کلّی این مسئله ( ۱۰۰$ برای ارایهٔ یک استراتژی پیروزی برای فرشتی با قدرت کافی، و ۱۰۰۰$ برای اثبات این که شیطان می تواند مستقل از قدرت فرشته پیروز شود ) . ابتدا پیشرفتهایی در ابعاد بالاتر صورت گرفت و اثبات های زیبایی ارائه شد. در سال ۲۰۰۶، مسئله اصلی حل شد و ثابت شد که فرشته می تواند پیروز شود.
مسئله ابتدا در سال ۱۹۸۲ در کتاب استراتژی برد نوشته برلکمپ، کانوی و گای، با نام «فرشته و مربّع خوار» منتشر شد. در فضای دو بعدی. چند نتیجه جزئی شامل:
• اگر فرشته قدرت ۱ داشته باشد، شیطان استراتژی پیروزی دارد ( کانوی، ۱۹۸۲ ) ( طبق گفته کانوی این نتیجه گیری متعلق به برلکمپ است )
• اگر فرشته هرگز مولفه yخود را افزایش ندهد، شیطان استراتژی پیروزی دارد. ( کانوی ۱۹۸۲ )
• اگر فرشته همواره فصلهٔ خود را از مبدأ زیاد کند، شیطان استراتژی پیروزی دارد ( کانوی. ۱۹۹۶ )

wiki: مسئله فرشته
