مسئله ی توریست منهتن ( به انگلیسی : Manhattan Tourist Problem به اختصار MTP ) یکی از مسائل مطرح در زمینه برنامه نویسی پویا است که در زمینه ی هم تراز کردن توالی ها بخصوص در بیوانفورماتیک کاربرد دارد. به طور خلاصه، هدف این مسئله یافتن مسیری از یک گره آغازین S به یک گره مقصد D در یک گراف توری ( Grid ) است به شکلی که از هرگره و یا یال حداکثر یکبار بگذریم و وزن مسیر حداکثر شود.
تصور کنید در محله ی منهتن نیویورک هستید و می خواهید از یک چهار راه به یک چهار راه دیگر بروید. از آنجایی که این محله یک قطب گردشگری است، در هر خیابان تعدادی جاذبه ی گردشگری موجود است. از آنجایی که شما میخواهید از حداکثر جاذبه های گردشگری دیدن کنید، مسیری را به مقصد بیابید که جمع تعداد جاذبه هایی که در خیابان هایی که از آن ها گذشته اید، حداکثر شود. [ ۱]
در این مسئله منظور از منهتن، یک گراف توری شکل است که مانند جدولی n در m است و نقطه ی ( 0 , 0 ) محل شروع مسیر و ( n , m ) نقطه ی پایان است. با توجه به شکل حرکت روی مسیر، می توان گفت که یال ها جهت دار و به سمت راست و یا پایین هستند و هر یال وزنی دارد که نشانگر تعداد جاذبه ها در خیابان نظیر آن است. [ ۲] [ ۳]
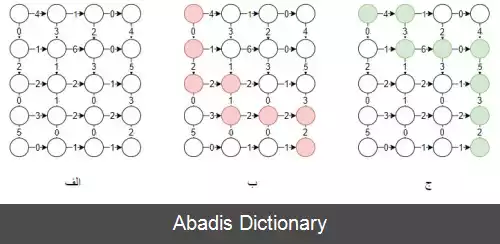
در شکل زیر یک نمونه مسئله ی توریست منهتن 4 در 3 مطرح شده و تعدادی از مسیر های ممکن، به علاوه ی مسیر جواب آورده شده:
در این روش، در هر مرحله، سنگین ترین یال را انتخاب می کنیم و مسیر را ادامه می دهیم. واضح است که چنین روشی همواره به جواب بهینه با جمع یال های حداکثر نمی رسد چرا که در بعضی گره ها، انتخاب یال با وزن کمتر در نهایت به وزن کلی بیشتری می رسد. با توجه به اینکه در مسیر توریست منهتن n در m از m + n گره عبور می کنیم، چنین الگوریتمی نیز از O ( n + m ) خواهد بود اما به جواب درستی نخواهد رسید.
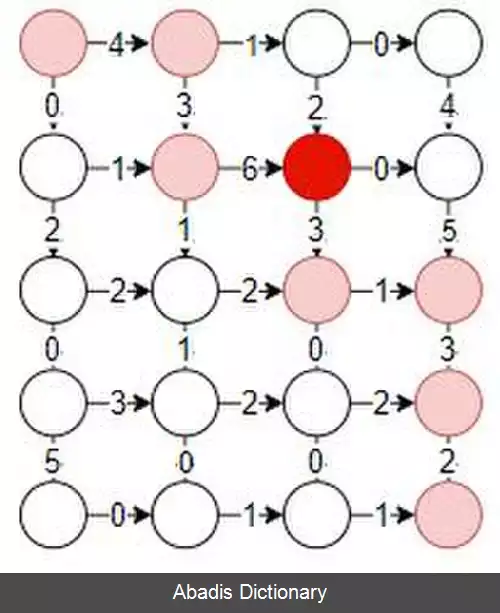
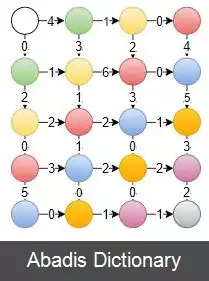
در این روش برای پیدا کردن بهترین مسیر به نقطه ی ( x , y ) باید بهترین مسیر به نقاط ( x − 1 , y ) و ( x , y − 1 ) را یافت و وزن هر کدام را با یالی که آن را به نقطه ی ( x , y ) جمع زد تا از بین آن دو بزرگترین مقدار به عنوان بهترین مسیر به ( x , y ) معرفی شود.
این الگوریتم اگرچه به یک جواب بهینه می رسد اما از نظر زمان الگوریتم مناسبی نیست چرا که وزن مسیر بهینه از مبدا تا یک نقطه، به دفعات زیاد محاسبه می شود. در واقع وزن مسیر از مبدا به ( x , y ) به ازای تمام نقاطی طول و عرضی بزرگتر از آن دارند نیز محاسبه می شود و این زمان اجرای الگوریتم را طولانی می کند. کد چنین روشی به زبان پایتون به شکل زیر است:
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتصور کنید در محله ی منهتن نیویورک هستید و می خواهید از یک چهار راه به یک چهار راه دیگر بروید. از آنجایی که این محله یک قطب گردشگری است، در هر خیابان تعدادی جاذبه ی گردشگری موجود است. از آنجایی که شما میخواهید از حداکثر جاذبه های گردشگری دیدن کنید، مسیری را به مقصد بیابید که جمع تعداد جاذبه هایی که در خیابان هایی که از آن ها گذشته اید، حداکثر شود. [ ۱]
در این مسئله منظور از منهتن، یک گراف توری شکل است که مانند جدولی n در m است و نقطه ی ( 0 , 0 ) محل شروع مسیر و ( n , m ) نقطه ی پایان است. با توجه به شکل حرکت روی مسیر، می توان گفت که یال ها جهت دار و به سمت راست و یا پایین هستند و هر یال وزنی دارد که نشانگر تعداد جاذبه ها در خیابان نظیر آن است. [ ۲] [ ۳]
در شکل زیر یک نمونه مسئله ی توریست منهتن 4 در 3 مطرح شده و تعدادی از مسیر های ممکن، به علاوه ی مسیر جواب آورده شده:
در این روش، در هر مرحله، سنگین ترین یال را انتخاب می کنیم و مسیر را ادامه می دهیم. واضح است که چنین روشی همواره به جواب بهینه با جمع یال های حداکثر نمی رسد چرا که در بعضی گره ها، انتخاب یال با وزن کمتر در نهایت به وزن کلی بیشتری می رسد. با توجه به اینکه در مسیر توریست منهتن n در m از m + n گره عبور می کنیم، چنین الگوریتمی نیز از O ( n + m ) خواهد بود اما به جواب درستی نخواهد رسید.
در این روش برای پیدا کردن بهترین مسیر به نقطه ی ( x , y ) باید بهترین مسیر به نقاط ( x − 1 , y ) و ( x , y − 1 ) را یافت و وزن هر کدام را با یالی که آن را به نقطه ی ( x , y ) جمع زد تا از بین آن دو بزرگترین مقدار به عنوان بهترین مسیر به ( x , y ) معرفی شود.
این الگوریتم اگرچه به یک جواب بهینه می رسد اما از نظر زمان الگوریتم مناسبی نیست چرا که وزن مسیر بهینه از مبدا تا یک نقطه، به دفعات زیاد محاسبه می شود. در واقع وزن مسیر از مبدا به ( x , y ) به ازای تمام نقاطی طول و عرضی بزرگتر از آن دارند نیز محاسبه می شود و این زمان اجرای الگوریتم را طولانی می کند. کد چنین روشی به زبان پایتون به شکل زیر است:




wiki: مسئله توریست منهتن
