تطابق سه بعدی در نظریه گراف تعمیم تطابق دوبخشی ( تطابق دوبعدی ) به ۳ ابرگراف یک شکل است. پیدا کردن بزرگ ترین تطابق سه بعدی یک مسئلۀ ان پی - سخت مشهور در نظریه پیچیدگی محاسباتی است.
فرض کنید X ، Y و Z مجموعه های متناهی مجزا باشند و T یک زیرمجموعه از Z × Y × X باشد. یعنی T شامل ۳ تایی های ( x , y , z ) است به طوری که X ∋ x ، Y ∋ y و Z ∋ z . T ⊇ M یک تطابق سه بعدی است در صورتی که به ازای هر دو سه تایی مجزا M ∋ ( x 1 , y 1 , z 1 ) و M ∋ ( x 2 , y 2 , z 2 ) داشته باشیم: x 2 ≠ x 1 ، y 2 ≠ y 1 و z 2 ≠ z 1 .
شکل سمت چپ صفحه تطابق های سه بعدی را نشان می دهد. X با نقاط قرمز، Y با نقاط آبی و Z با نقاط سبز نشان داده شده است. شکل الف مجموعۀ T ( نواحی خاکستری ) را نشان می دهد. شکل ب یک تطابق سه بعدی M با ۲ = | M | را نشان می دهد و شکل پ یک تطابق سه بعدی M با ۳ = | M | را نشان می دهد.
تطابق M که در شکل پ نشان داده شده است یک تطابق سه بعدی بیشینه است، یعنی | M | را بیشینه می کند. تطابق های نشان داده شده در شکل های ب و پ تطابق های سه بعدی ماکسیمال هستند، یعنی نمی توان با افزودن عضوهای بیش تری از T آن ها را گسترش داد.
یک تطابق دوبعدی را می توان به طور کاملاً مشابه تعریف کرد. فرض کنید X و Y مجموعه های متناهی مجزا باشند و T یک زیرمجموعه از X × Y باشد. T ⊇ M یک تطابق دوبعدی است در صورتی که برای هر دو زوج مجزای M ∋ ( x 1 , y 1 ) و M ∋ ( x 2 , y 2 ) داشته باشیم: x 2 ≠ x 1 و y 2 ≠ y 1 .
در تطابق دوبعدی، مجموعۀ T را می توان به صورت مجموعۀ یال ها در یک گراف دوبخشی ( X , Y , T ) = G تعبیر کرد؛ هر یال T یک رأس از X را به یک رأس از Y متصل می کند و یک تطابق دوبعدی یک تطابق در گراف G است، یعنی مجموعه ای از یال های دوبه دو غیرمجاور.
از این رو تطابق های سه بعدی را می توان به صورت تعمیم تطابق به ابرگراف ها تعبیر کرد: مجموعه های X ، Y و Z شامل یال ها هستند، هر عضو T یک ابرگراف است و مجموعۀ M شامل یال های دوبه دو غیرمجاور است ( یال هایی که رأس مشترک ندارند ) .
یک تطابق سه بعدی حالت خاصی از یک بسته بندی مجموعه است: می توانیم هر عضو ( x , y , z ) از T را به عنوان یک زیرمجموعۀ { x , y , z } از Z ∪ Y ∪ X تعبیر کنیم؛ پس یک تطابق سه بعدی M شامل زیرمجموعه های دوبه دو مجزا است.
در نظریه پیچیدگی محاسباتی، تطابق سه بعدی هم چنین نام مسئله تصمیم زیر است: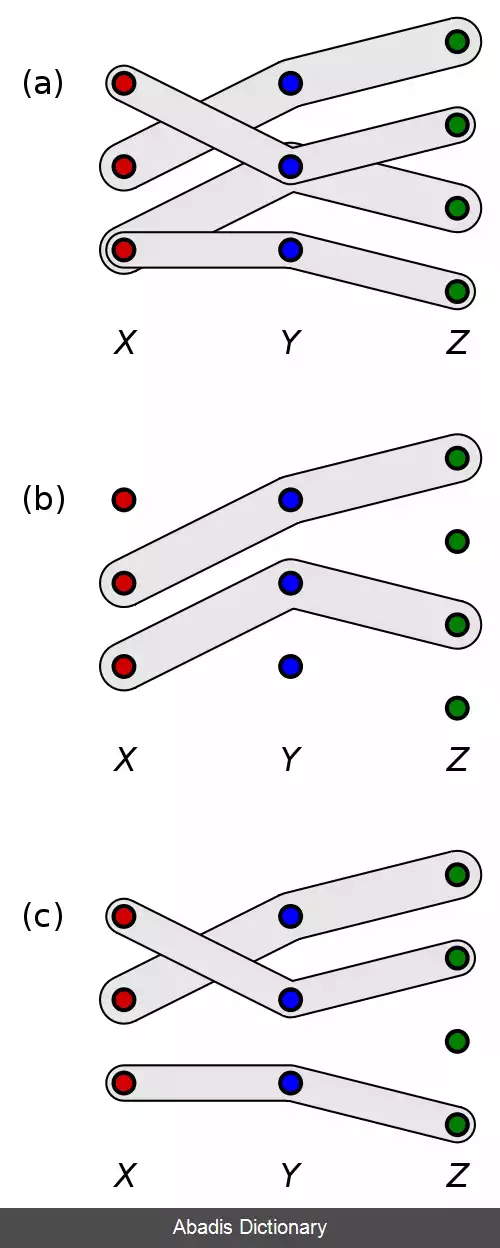
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنید X ، Y و Z مجموعه های متناهی مجزا باشند و T یک زیرمجموعه از Z × Y × X باشد. یعنی T شامل ۳ تایی های ( x , y , z ) است به طوری که X ∋ x ، Y ∋ y و Z ∋ z . T ⊇ M یک تطابق سه بعدی است در صورتی که به ازای هر دو سه تایی مجزا M ∋ ( x 1 , y 1 , z 1 ) و M ∋ ( x 2 , y 2 , z 2 ) داشته باشیم: x 2 ≠ x 1 ، y 2 ≠ y 1 و z 2 ≠ z 1 .
شکل سمت چپ صفحه تطابق های سه بعدی را نشان می دهد. X با نقاط قرمز، Y با نقاط آبی و Z با نقاط سبز نشان داده شده است. شکل الف مجموعۀ T ( نواحی خاکستری ) را نشان می دهد. شکل ب یک تطابق سه بعدی M با ۲ = | M | را نشان می دهد و شکل پ یک تطابق سه بعدی M با ۳ = | M | را نشان می دهد.
تطابق M که در شکل پ نشان داده شده است یک تطابق سه بعدی بیشینه است، یعنی | M | را بیشینه می کند. تطابق های نشان داده شده در شکل های ب و پ تطابق های سه بعدی ماکسیمال هستند، یعنی نمی توان با افزودن عضوهای بیش تری از T آن ها را گسترش داد.
یک تطابق دوبعدی را می توان به طور کاملاً مشابه تعریف کرد. فرض کنید X و Y مجموعه های متناهی مجزا باشند و T یک زیرمجموعه از X × Y باشد. T ⊇ M یک تطابق دوبعدی است در صورتی که برای هر دو زوج مجزای M ∋ ( x 1 , y 1 ) و M ∋ ( x 2 , y 2 ) داشته باشیم: x 2 ≠ x 1 و y 2 ≠ y 1 .
در تطابق دوبعدی، مجموعۀ T را می توان به صورت مجموعۀ یال ها در یک گراف دوبخشی ( X , Y , T ) = G تعبیر کرد؛ هر یال T یک رأس از X را به یک رأس از Y متصل می کند و یک تطابق دوبعدی یک تطابق در گراف G است، یعنی مجموعه ای از یال های دوبه دو غیرمجاور.
از این رو تطابق های سه بعدی را می توان به صورت تعمیم تطابق به ابرگراف ها تعبیر کرد: مجموعه های X ، Y و Z شامل یال ها هستند، هر عضو T یک ابرگراف است و مجموعۀ M شامل یال های دوبه دو غیرمجاور است ( یال هایی که رأس مشترک ندارند ) .
یک تطابق سه بعدی حالت خاصی از یک بسته بندی مجموعه است: می توانیم هر عضو ( x , y , z ) از T را به عنوان یک زیرمجموعۀ { x , y , z } از Z ∪ Y ∪ X تعبیر کنیم؛ پس یک تطابق سه بعدی M شامل زیرمجموعه های دوبه دو مجزا است.
در نظریه پیچیدگی محاسباتی، تطابق سه بعدی هم چنین نام مسئله تصمیم زیر است:

wiki: مسئله تطابق سه بعدی
