مسئله تانک آلمانی. در نظریه آماری تخمین، مسئله تانک آلمانی به تخمین حداکثر در یک توزیع یکنواخت گسسته از نمونه برداری بدون جایگزینی گفته می شود. به عبارت ساده، فرض کنید تعداد نامعینی از اشیا داریم که به ترتیب از ۱ تا N شماره گذاری می شوند. نمونه ای تصادفی از این موارد را می گیریم و عدد آنها را مشاهده می کنیم. مساله در اینجا تخمین N بر اساس این اعداد مشاهده شده است.
این مساله پس از اعمال آن توسط نیروهای متفقین در جنگ جهانی دوم و تخمین میزان ماهانه تولید تانک آلمانی بر اساس داده های اندک نامگذاری شده است. در این کار آنها از روش ساخت و اختصاص اعداد صعودی برای شماره سریال بخش های یک تانک ( شاسی، گیربکس، موتور، چرخ ) استفاده کردند، از آنجایی که تعدادی تانک آلمانی در جنگ جهانی دوم بدستان متفقین افتاد، آنها تعداد کل تانک های آلمان را با تقریب خوبی تخمین زدند.
این مساله را می توان با استفاده از استنتاج فراوانی گرایانه یا استنتاج بیزی، حل کرد که نتایج متفاوتی می دهند. برآورد حداکثر جمعیت بر اساس یک نمونه، نتایج واگرای متفاوتی را می دهد، در حالی که تخمین بر اساس چند نمونه، یک سؤال خوب است که پاسخ آن ساده است ( به خصوص در استنتاج فراوانی گرایانه ) اما بدیهی نیست ( به خصوص در استنتاج بیزی ) .
فرض کنید چهار تانک بدستمان افتاده است، و شماره سریال آنها این است: "۱۹"، "۴۰"، "۴۲" و "۶۰".
روش فراوانی گرایانه این تعداد تانک را به ما می دهد:
استنتاج بیزی، اگر از میانه استفاده کنید، به تخمین فراوانی گرایانه نزدیک است:
در حالی که استنتاج بیزی مبتنی بر میانگین کاملاً دور است:
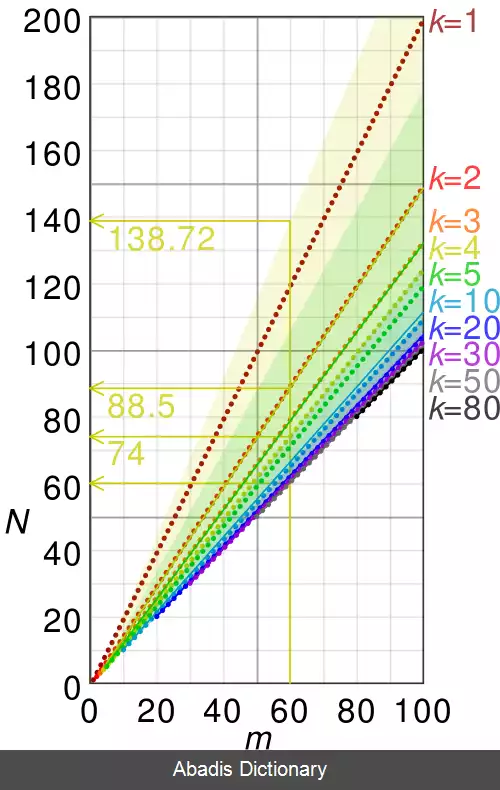
اگر k = ۴ ( تعداد تانک ) و m = ۶۰ ( بزرگترین شماره سریال ) در نظر بگیریم حداکثر تعداد تانک مشاهده شده از این تخمین بدست می آید:
تخمین ۷۴٫۵ ( میانه ) و ۸۹ ( میانگین ) بدین صورت در استنناج بیزی محاسبه می شود:
در حقیقت، در هر دو استنتاج بیزی مبتنی بر تابع جرم احتمال زیر است:
این توزیع دارای چولگی مثبت است و مربوط به این واقعیت است که حداقل ۶۰ تانک وجود دارد. به دلیل همین چولگی، ممکن است میانگین معنی دارترین تخمین نباشد. میانه در این مثال ۷۴٫۵، شباهت بیشتری به استنتاج فراوانی گرایانه دارد. با استفاده از تقریب استرلینگ، تابع احتمال بیزی به این تقریب زده می شود:
که تقریب زیر برای میانه را می دهد:
سرانجام، تخمین متوسط توسط بیزی و انحراف آن به شرح زیر محاسبه می شود:
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین مساله پس از اعمال آن توسط نیروهای متفقین در جنگ جهانی دوم و تخمین میزان ماهانه تولید تانک آلمانی بر اساس داده های اندک نامگذاری شده است. در این کار آنها از روش ساخت و اختصاص اعداد صعودی برای شماره سریال بخش های یک تانک ( شاسی، گیربکس، موتور، چرخ ) استفاده کردند، از آنجایی که تعدادی تانک آلمانی در جنگ جهانی دوم بدستان متفقین افتاد، آنها تعداد کل تانک های آلمان را با تقریب خوبی تخمین زدند.
این مساله را می توان با استفاده از استنتاج فراوانی گرایانه یا استنتاج بیزی، حل کرد که نتایج متفاوتی می دهند. برآورد حداکثر جمعیت بر اساس یک نمونه، نتایج واگرای متفاوتی را می دهد، در حالی که تخمین بر اساس چند نمونه، یک سؤال خوب است که پاسخ آن ساده است ( به خصوص در استنتاج فراوانی گرایانه ) اما بدیهی نیست ( به خصوص در استنتاج بیزی ) .
فرض کنید چهار تانک بدستمان افتاده است، و شماره سریال آنها این است: "۱۹"، "۴۰"، "۴۲" و "۶۰".
روش فراوانی گرایانه این تعداد تانک را به ما می دهد:
استنتاج بیزی، اگر از میانه استفاده کنید، به تخمین فراوانی گرایانه نزدیک است:
در حالی که استنتاج بیزی مبتنی بر میانگین کاملاً دور است:
اگر k = ۴ ( تعداد تانک ) و m = ۶۰ ( بزرگترین شماره سریال ) در نظر بگیریم حداکثر تعداد تانک مشاهده شده از این تخمین بدست می آید:
تخمین ۷۴٫۵ ( میانه ) و ۸۹ ( میانگین ) بدین صورت در استنناج بیزی محاسبه می شود:
در حقیقت، در هر دو استنتاج بیزی مبتنی بر تابع جرم احتمال زیر است:
این توزیع دارای چولگی مثبت است و مربوط به این واقعیت است که حداقل ۶۰ تانک وجود دارد. به دلیل همین چولگی، ممکن است میانگین معنی دارترین تخمین نباشد. میانه در این مثال ۷۴٫۵، شباهت بیشتری به استنتاج فراوانی گرایانه دارد. با استفاده از تقریب استرلینگ، تابع احتمال بیزی به این تقریب زده می شود:
که تقریب زیر برای میانه را می دهد:
سرانجام، تخمین متوسط توسط بیزی و انحراف آن به شرح زیر محاسبه می شود:


wiki: مسئله تانک آلمانی
