در تئوری بهینه سازی، مسائل بیشینه جریان شامل پیدا کردن یک جریان عملی بیشینه از داخل یک شبکهٔ جریان تک - مبدأ و تک - مقصد است. می توان به مسئلهٔ بیشینه جریان، به صورت حالت خاصی از مسائل پیچیده تر شبکهٔ جریان، مانند مسئلهٔ گردش، نگاه کرد. مقدار ماکسیمم یک جریان s - t ( جریان از مبدأ به مقصد ) برابر حداقل ظرفیت یک برش s - t ( برشی که مبدأ را از مقصد جدا می کند ) در شبکه است، همان طور که در قضیهٔ جریان بیشینه - برش کمینه ذکر شده است.
مسئلهٔ بیشینهٔ جریان ابتدا توسط T. E. Harris و F. S. Ross در سال ۱۹۵۴ به عنوان مدل ساده شده ای از جریان رفت و آمد خط آهن شوروی مطرح شد. در ۱۹۵۵، . Lester R. Ford, Jr و Delbert R. Fulkerson اولین الگوریتم شناخته شده، الگوریتم فورد–فالکرسون را ایجاد کردند. در طول زمان، تعداد زیادی راه حل بهبود یافته برای مسئلهٔ بیشینهٔ جریان پیدا شده است، به ویژه الگوریتم کوتاه ترین راه افزوده از Edmonds و Karp و به صورت مستقل از Dinitz، الگوریتم سد کردن جریان Dinitz، الگوریتم ارسال - برچسب Goldberg و Tarjan، و الگوریتم سد کردن دودویی جریان از Goldberg و Rao. الگوریتم جریان الکتریکی Madry، Kelner، Christano و Spielman یک جریان بیشینهٔ تقریباً بهینه می یابد اما فقط در گراف های بدون جهت کار می کند.
فرض کنید N = ( V , E ) یک شبکه است با s , t ∈ V که به ترتیب مبدأ و مقصد هستند.
• f u v ≤ c u v {\displaystyle \scriptstyle f_{uv}\leq c_{uv}} به ازای هر ( u , v ) ∈ E {\displaystyle \scriptstyle ( u, v ) \in E} ( شرط ظرفیت: جریان یک یال نمی تواند از ظرفیتش بیشتر باشد )
• ∑ u : ( u , v ) ∈ E f u v = ∑ u : ( v , u ) ∈ E f v u {\displaystyle \scriptstyle \sum _{u: ( u, v ) \in E}f_{uv}=\sum _{u: ( v, u ) \in E}f_{vu}} به ازای هر v ∈ V ∖ { s , t } {\displaystyle \scriptstyle v\in V\setminus \{s, t\}} ( بقای جریان ها: جمع جریان های ورودی یک رأس باید با جمع جریان های خروجی از آن برابر باشد، به جز در رأس های مبدأ و مقصد )
مسئلهٔ بیشینه جریان، بیشینه کردن | f | است، یعنی هدایت بیش ترین جریان ممکن از به .
می توان گراف باقیمانده را تعریف کرد تا راهی اصولی برای جستجو کردن عملیات های جلو - عقب برای یافتن بیشینه جریان فراهم کند. اگر شبکهٔ جریان G و جریان f روی G را داشته باشیم، G f ، گراف باقیماندهٔ G را با توجه به f اینگونه تعریف می کنیم: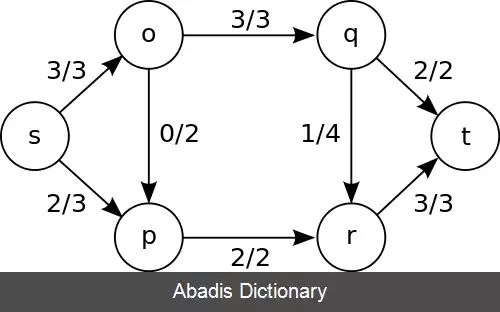
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمسئلهٔ بیشینهٔ جریان ابتدا توسط T. E. Harris و F. S. Ross در سال ۱۹۵۴ به عنوان مدل ساده شده ای از جریان رفت و آمد خط آهن شوروی مطرح شد. در ۱۹۵۵، . Lester R. Ford, Jr و Delbert R. Fulkerson اولین الگوریتم شناخته شده، الگوریتم فورد–فالکرسون را ایجاد کردند. در طول زمان، تعداد زیادی راه حل بهبود یافته برای مسئلهٔ بیشینهٔ جریان پیدا شده است، به ویژه الگوریتم کوتاه ترین راه افزوده از Edmonds و Karp و به صورت مستقل از Dinitz، الگوریتم سد کردن جریان Dinitz، الگوریتم ارسال - برچسب Goldberg و Tarjan، و الگوریتم سد کردن دودویی جریان از Goldberg و Rao. الگوریتم جریان الکتریکی Madry، Kelner، Christano و Spielman یک جریان بیشینهٔ تقریباً بهینه می یابد اما فقط در گراف های بدون جهت کار می کند.
فرض کنید N = ( V , E ) یک شبکه است با s , t ∈ V که به ترتیب مبدأ و مقصد هستند.
• f u v ≤ c u v {\displaystyle \scriptstyle f_{uv}\leq c_{uv}} به ازای هر ( u , v ) ∈ E {\displaystyle \scriptstyle ( u, v ) \in E} ( شرط ظرفیت: جریان یک یال نمی تواند از ظرفیتش بیشتر باشد )
• ∑ u : ( u , v ) ∈ E f u v = ∑ u : ( v , u ) ∈ E f v u {\displaystyle \scriptstyle \sum _{u: ( u, v ) \in E}f_{uv}=\sum _{u: ( v, u ) \in E}f_{vu}} به ازای هر v ∈ V ∖ { s , t } {\displaystyle \scriptstyle v\in V\setminus \{s, t\}} ( بقای جریان ها: جمع جریان های ورودی یک رأس باید با جمع جریان های خروجی از آن برابر باشد، به جز در رأس های مبدأ و مقصد )
مسئلهٔ بیشینه جریان، بیشینه کردن | f | است، یعنی هدایت بیش ترین جریان ممکن از به .
می توان گراف باقیمانده را تعریف کرد تا راهی اصولی برای جستجو کردن عملیات های جلو - عقب برای یافتن بیشینه جریان فراهم کند. اگر شبکهٔ جریان G و جریان f روی G را داشته باشیم، G f ، گراف باقیماندهٔ G را با توجه به f اینگونه تعریف می کنیم:






wiki: مسئله بیشینه جریان
