بزرگترین زیردنباله مشترک ( به انگلیسی: Longest Common Subsequence ) ، روشی است که برای پیدا کردن بزرگترین زیردنباله در مجموعه ای از دنباله ها ( غالباً دو دنباله ) به کار می رود و مسئله ای قدیمی در علم کامپیوتر است. تفاوت این مسئله با مسئله ی بزرگترین زیررشته ی مشترک در این است که برای یک زیردنباله از یک رشته، نیازی نیست که اعضای آن مجاور یک دیگر باشند و به طور متوالی آمده باشند. این مسئله اساس کار برنامه های مقایسه کننده فایل است که تفاوت دو فایل را نمایش می دهد. همین طور در بیوانفورماتیک برای مقایسه رشته های دی ان ای کاربرد دارد.
در علوم کامپیوتر، مسئله بلندترین زیررشته مشترک برای یافتن بلندترین رشته ( یا رشته هایی ) که زیر رشته ( یا زیررشته هایی ) از دویاچندین رشته هستند، می باشد. این مسئله نباید با مسئله بلندترین زیردنباله مشترک اشتباه گرفته شود. ( برای توضیحی در مورد تفاوت میان یک زیررشته و یک زیردنباله به زیررشته درمقابل زیردنباله رجوع کنید ) .
دو رشته زیر را در نظر بگیرید:
S 1 = A C C G G T C G A G T G C G C G G A G C C G G C C G A A
S 2 = G T C G T T C G G A A T G C C G T T G C T C T G T A A A
هدف مقایسه این دو رشته و پیدا کردن شباهت بین آن ها است. بزرگترین زیردنباله مشترک این طور تعریف می شود که دنباله ای مانند S 3 است به طوری که حروف موجود در S 3 با حفظ ترتیب در S 1 و S 2 موجود باشد. اما مطلقاً لزومی ندارد که متوالی باشد. از طرفی S 3 باید بزرگترین دنباله ممکن با خواص بالا باشد. به طور کلی اگر دو رشته X = ⟨ x 1 , x 2 , . . . , x n ⟩ و Y = ⟨ y 1 , y 2 , . . . , y n ⟩ را در نظر بگیریم، یک بلندترین زیر دنباله مشترک را می توان با استفاده از برنامه نویسی پویا پیدا کرد.
مسئله LCS دارای خصوصیت زیر ساختار بهینه ( Optimal Substructure ) است:
مسئله LCS را می توان به زیر مسئله های کوچک تر تقسیم نمود.
که این زیر مسئله ها جفت دنباله های پیشوندی دو دنباله ورودی هستند. اگر داشته باشیم: X = ⟨ x 1 , x 2 , . . . , x n ⟩ ٫ آن گاه X i به این صورت تعریف می شود: X i = ⟨ x 1 , x 2 , . . . , x i ⟩
فرض کنید X = ⟨ x 1 , x 2 , . . . , x m ⟩ و Y = ⟨ y 1 , y 2 , . . . , y n ⟩ دو رشته باشند و Z = ⟨ z 1 , z 2 , . . . , z k ⟩ بلندترین زیردنباله مشترک یا LCS دو رشته Y و X باشند. پیاده سازی الگوریتم با استفاده از روش برنامه نویسی پویا به این صورت است: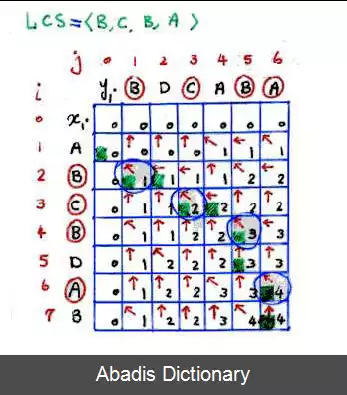

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر علوم کامپیوتر، مسئله بلندترین زیررشته مشترک برای یافتن بلندترین رشته ( یا رشته هایی ) که زیر رشته ( یا زیررشته هایی ) از دویاچندین رشته هستند، می باشد. این مسئله نباید با مسئله بلندترین زیردنباله مشترک اشتباه گرفته شود. ( برای توضیحی در مورد تفاوت میان یک زیررشته و یک زیردنباله به زیررشته درمقابل زیردنباله رجوع کنید ) .
دو رشته زیر را در نظر بگیرید:
S 1 = A C C G G T C G A G T G C G C G G A G C C G G C C G A A
S 2 = G T C G T T C G G A A T G C C G T T G C T C T G T A A A
هدف مقایسه این دو رشته و پیدا کردن شباهت بین آن ها است. بزرگترین زیردنباله مشترک این طور تعریف می شود که دنباله ای مانند S 3 است به طوری که حروف موجود در S 3 با حفظ ترتیب در S 1 و S 2 موجود باشد. اما مطلقاً لزومی ندارد که متوالی باشد. از طرفی S 3 باید بزرگترین دنباله ممکن با خواص بالا باشد. به طور کلی اگر دو رشته X = ⟨ x 1 , x 2 , . . . , x n ⟩ و Y = ⟨ y 1 , y 2 , . . . , y n ⟩ را در نظر بگیریم، یک بلندترین زیر دنباله مشترک را می توان با استفاده از برنامه نویسی پویا پیدا کرد.
مسئله LCS دارای خصوصیت زیر ساختار بهینه ( Optimal Substructure ) است:
مسئله LCS را می توان به زیر مسئله های کوچک تر تقسیم نمود.
که این زیر مسئله ها جفت دنباله های پیشوندی دو دنباله ورودی هستند. اگر داشته باشیم: X = ⟨ x 1 , x 2 , . . . , x n ⟩ ٫ آن گاه X i به این صورت تعریف می شود: X i = ⟨ x 1 , x 2 , . . . , x i ⟩
فرض کنید X = ⟨ x 1 , x 2 , . . . , x m ⟩ و Y = ⟨ y 1 , y 2 , . . . , y n ⟩ دو رشته باشند و Z = ⟨ z 1 , z 2 , . . . , z k ⟩ بلندترین زیردنباله مشترک یا LCS دو رشته Y و X باشند. پیاده سازی الگوریتم با استفاده از روش برنامه نویسی پویا به این صورت است:


