مسئله ازدواج پایدار در ریاضیات برای مدل سازی تطابق پایدار به کار می رود.
به طور کلی این قضیه بیانگر این است که اگر مجموعه ای از مردها و مجوعه ای از زن ها داشته باشیم که هر یک دارای اولویت هایی برای ازدواج باشند، در این راستا حتماً راهی وجود داردکه در نهایت امکان ندارد دو نفر که یکدیگر را می خواهند ( در واقع در اولویت یکدیگر هستند ) با یکدیگر نباشند. این راه از طریق الگوریتم گیل - شاپلی پیدا می شود. توجه کنید که طبق این الگوریتم حتماً راهی وجود دارد که شرایط بالا را داشته باشد.
در شکل روبه رو: ۴ مرد ( شاه ) و ۴ زن ( ملکه ) وجود دارند. برای مثال مرد A زن ها را با ترتیب C , A، D , B امتیاز دهی کرده است و به همان صورت زن B مردها را با ترتیب A , B، D , C ترجیح می دهد.
در سال ۱۹۶۲ دیوید گیل و لوید شاپلی اثبات کردند که برای هر تعداد مساوی زن و مرد، می توان مسئلهٔ ازدواج پایدار را حل کرد و الگوریتمی برای این کار ارائه دادند. هدف از اجرای این الگوریتم آن است که راهی پایدار برای تطبیق دادن و جفت کردن مردان با زنان ( با توجه به اولویت های آن ها ) بیابیم. مرتبه زمانی این الگوریتم ( O ( n2 می باشد.
راهی ناپایدار است که در آن مرد و زنی وجود داشته باشند که با یکدیگر جفت نشده اند اما یکدیگر را به جفت های فعلی خود ترجیح دهند.
همان طور که می بینیم این یک انتخاب ناپایدار است. به مرد C و زن B نگاه کنید. هر دوی آن ها یکدیگر را به جفت های فعلی خود ترجیح می دهند. مرد C با انتخاب دوم خود جفت شده و زن B با انتخاب سوم خود، در حالی که اگر این دو با هم جفت می شدند هر دو به انتخاب اول خود می رسیدند. قلب ها نشان دهندهٔ بی ثبات بودن انتخاب های کنونی می باشند.
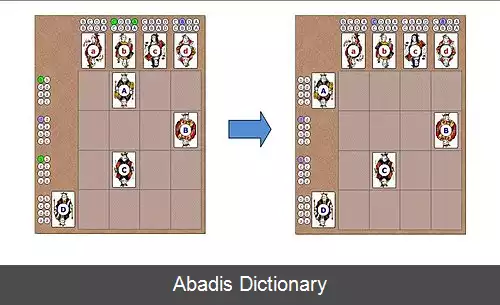
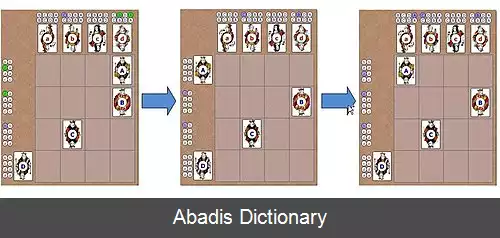
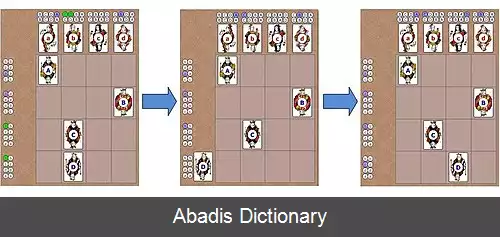
پیدا کردن راهی پایدار برای جفت کردن مردها و زنها نیازمند آزمایش های متعدد است که گاه زمان زیادی می برد اما الگوریتم گیل - شاپلی راه حلی را برای یک انتخاب پایدار ارائه می کند. این الگوریتم بیانگر این است که بدون توجه یه تعداد مردها و زن ها، همواره می توان راهی پایدار برای جفت کردن آن ها پیدا کرد. طرز کار این الگوریتم به صورت زیر است: ابتدا هر مرد از اولویت اول خود درخواست می کند، اگر زن مورد نظر قبلاً با کسی «نامزد» نشده باشد این درخواست را قبول می کند اما اگر فرد دیگری نیز از او درخواست کرده بود، زن شخصی را برمی گزیند که اولویت بالاتری نسبت به فرد دیگر دارد. مردی که درخواستش رد شده است از این درخواست صرف نظر کرده و درخواست دیگری را به اولویت بعدی خود مطرح می کند. در مثال زیر این روش مشخص تر است: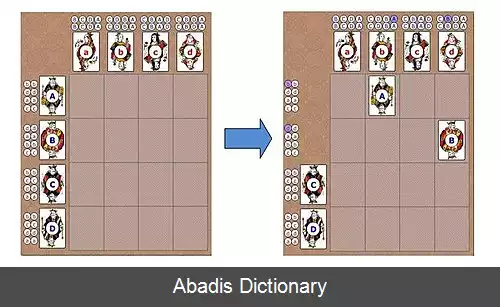
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه طور کلی این قضیه بیانگر این است که اگر مجموعه ای از مردها و مجوعه ای از زن ها داشته باشیم که هر یک دارای اولویت هایی برای ازدواج باشند، در این راستا حتماً راهی وجود داردکه در نهایت امکان ندارد دو نفر که یکدیگر را می خواهند ( در واقع در اولویت یکدیگر هستند ) با یکدیگر نباشند. این راه از طریق الگوریتم گیل - شاپلی پیدا می شود. توجه کنید که طبق این الگوریتم حتماً راهی وجود دارد که شرایط بالا را داشته باشد.
در شکل روبه رو: ۴ مرد ( شاه ) و ۴ زن ( ملکه ) وجود دارند. برای مثال مرد A زن ها را با ترتیب C , A، D , B امتیاز دهی کرده است و به همان صورت زن B مردها را با ترتیب A , B، D , C ترجیح می دهد.
در سال ۱۹۶۲ دیوید گیل و لوید شاپلی اثبات کردند که برای هر تعداد مساوی زن و مرد، می توان مسئلهٔ ازدواج پایدار را حل کرد و الگوریتمی برای این کار ارائه دادند. هدف از اجرای این الگوریتم آن است که راهی پایدار برای تطبیق دادن و جفت کردن مردان با زنان ( با توجه به اولویت های آن ها ) بیابیم. مرتبه زمانی این الگوریتم ( O ( n2 می باشد.
راهی ناپایدار است که در آن مرد و زنی وجود داشته باشند که با یکدیگر جفت نشده اند اما یکدیگر را به جفت های فعلی خود ترجیح دهند.
همان طور که می بینیم این یک انتخاب ناپایدار است. به مرد C و زن B نگاه کنید. هر دوی آن ها یکدیگر را به جفت های فعلی خود ترجیح می دهند. مرد C با انتخاب دوم خود جفت شده و زن B با انتخاب سوم خود، در حالی که اگر این دو با هم جفت می شدند هر دو به انتخاب اول خود می رسیدند. قلب ها نشان دهندهٔ بی ثبات بودن انتخاب های کنونی می باشند.
پیدا کردن راهی پایدار برای جفت کردن مردها و زنها نیازمند آزمایش های متعدد است که گاه زمان زیادی می برد اما الگوریتم گیل - شاپلی راه حلی را برای یک انتخاب پایدار ارائه می کند. این الگوریتم بیانگر این است که بدون توجه یه تعداد مردها و زن ها، همواره می توان راهی پایدار برای جفت کردن آن ها پیدا کرد. طرز کار این الگوریتم به صورت زیر است: ابتدا هر مرد از اولویت اول خود درخواست می کند، اگر زن مورد نظر قبلاً با کسی «نامزد» نشده باشد این درخواست را قبول می کند اما اگر فرد دیگری نیز از او درخواست کرده بود، زن شخصی را برمی گزیند که اولویت بالاتری نسبت به فرد دیگر دارد. مردی که درخواستش رد شده است از این درخواست صرف نظر کرده و درخواست دیگری را به اولویت بعدی خود مطرح می کند. در مثال زیر این روش مشخص تر است:




wiki: مسئله ازدواج پایدار
