مسئله P در مقابل NP. اگر چک کردن صحت حل یک مسئله آسان باشد، آیا لزوماً حل آن مسئله نیز آسان است؟
چندجمله ای P در مقابل NP ( به انگلیسی: P versus NP Problem ) ، مسئله حل نشده مهمی در علوم کامپیوتر است. این مسئله می پرسد که آیا هر مسئله ای که صحت جواب های آن را بتوان به سرعت ارزیابی نمود، به سرعت هم قابل حل شدن است؟ این مسئله یکی از مسائل جایزه هزاره بوده که توسط مؤسسه ریاضیاتی کِلِی انتخاب شده و برای نخستین کسی که به آن پاسخ درست دهد، جایزه یک میلیون دلاری تعیین شده است. [ نیازمند منبع]
اصطلاح به سرعت ارزیابی و حل شدن مسائل، که در توصیف این مسئله به کار رفت، در علوم کامپیوتر به معنای این است که الگوریتمی برای آن وجود دارد که زمان اجرای آن چندجمله ای است، چنان که زمان لازم جهت تکمیل وظیفه بر حسب اندازه ورودی الگوریتم، تابع چندجمله ای است ( در مقابل مرتبه زمانی نمایی ) . به کلاس کلی مسائلی که بتوان برایشان الگوریتمی با زمان اجرای چندجمله ای ارائه نمود، «کلاس P» یا صرفاً «P» گفته می شود. برای برخی مسائل راه شناخته شده ای جهت یافتن سریع پاسخ ها وجود ندارد، اما می توان جواب های پیشنهادی را به سرعت ارزیابی کرد. کلاس مسائلی که بتوان پاسخ های پیشنهادیشان را به سرعت ارزیابی کرد را NP نامیده که مخفف Nondeterministic Polynomical time بوده که ترجمه تحت اللفظی آن به صورت «زمان چندجمله ای غیرقطعی» ( یا زمان اجرای چندجمله ای غیرقطعی ) است. [ یادداشت ها ۱]
جواب به سؤال P در مقابل NP تعیین خواهد کرد که آیا مسائل قابل ارزیابی در زمان چندجمله ای را می توان در زمان چندجمله ای نیز حل نمود یا خیر. اگر مشخص شود که P ≠ N P است ( چنان که باور عموم نیز بر همین مبناست ) ، به این معنا خواهد بود که مسائلی در NP وجود دارند ه محاسبه آن از ارزیابی اش دشوارتر است: یعنی نمی توان آن ها را در زمان چندجمله ای حل کرد، اما جواب هایش را می توان در زمان چندجمله ای حل نمود.
جدا از مهم بودن این مسئله در نظریه محاسبه، اثبات هر کدام از دو حالت ممکن آن دارای پی آمدهای ژرفی در ریاضیات، رمزنگاری، الگوریتم جست و جو، هوش مصنوعی، نظریه بازی ها، پردازش چندرسانه ای، فلسفه، اقتصاد و سایر زمینه هاست. [ ۲]
ارتباط بین کلاس های پیچیدگی P و NP در نظریه پیچیدگی محاسباتی - بخشی از نظریه محاسبات که به بررسی منابع مورد نیاز در زمان محاسبه جواب یک مسئله می پردازد - مطالعه می شود. مهم ترین منابع یکی زمان ( مراحل یا گام های مورد نیاز برای دستیابی به جواب ) و دیگری فضا ( حافظه مورد نیاز برای حل مسئله ) است.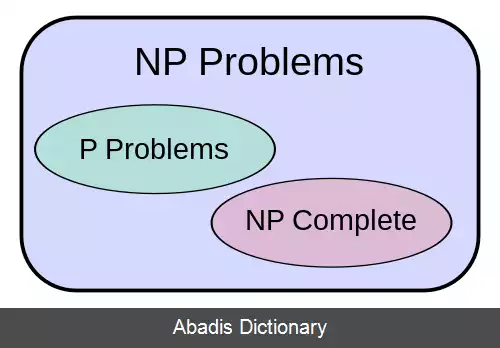
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفچندجمله ای P در مقابل NP ( به انگلیسی: P versus NP Problem ) ، مسئله حل نشده مهمی در علوم کامپیوتر است. این مسئله می پرسد که آیا هر مسئله ای که صحت جواب های آن را بتوان به سرعت ارزیابی نمود، به سرعت هم قابل حل شدن است؟ این مسئله یکی از مسائل جایزه هزاره بوده که توسط مؤسسه ریاضیاتی کِلِی انتخاب شده و برای نخستین کسی که به آن پاسخ درست دهد، جایزه یک میلیون دلاری تعیین شده است. [ نیازمند منبع]
اصطلاح به سرعت ارزیابی و حل شدن مسائل، که در توصیف این مسئله به کار رفت، در علوم کامپیوتر به معنای این است که الگوریتمی برای آن وجود دارد که زمان اجرای آن چندجمله ای است، چنان که زمان لازم جهت تکمیل وظیفه بر حسب اندازه ورودی الگوریتم، تابع چندجمله ای است ( در مقابل مرتبه زمانی نمایی ) . به کلاس کلی مسائلی که بتوان برایشان الگوریتمی با زمان اجرای چندجمله ای ارائه نمود، «کلاس P» یا صرفاً «P» گفته می شود. برای برخی مسائل راه شناخته شده ای جهت یافتن سریع پاسخ ها وجود ندارد، اما می توان جواب های پیشنهادی را به سرعت ارزیابی کرد. کلاس مسائلی که بتوان پاسخ های پیشنهادیشان را به سرعت ارزیابی کرد را NP نامیده که مخفف Nondeterministic Polynomical time بوده که ترجمه تحت اللفظی آن به صورت «زمان چندجمله ای غیرقطعی» ( یا زمان اجرای چندجمله ای غیرقطعی ) است. [ یادداشت ها ۱]
جواب به سؤال P در مقابل NP تعیین خواهد کرد که آیا مسائل قابل ارزیابی در زمان چندجمله ای را می توان در زمان چندجمله ای نیز حل نمود یا خیر. اگر مشخص شود که P ≠ N P است ( چنان که باور عموم نیز بر همین مبناست ) ، به این معنا خواهد بود که مسائلی در NP وجود دارند ه محاسبه آن از ارزیابی اش دشوارتر است: یعنی نمی توان آن ها را در زمان چندجمله ای حل کرد، اما جواب هایش را می توان در زمان چندجمله ای حل نمود.
جدا از مهم بودن این مسئله در نظریه محاسبه، اثبات هر کدام از دو حالت ممکن آن دارای پی آمدهای ژرفی در ریاضیات، رمزنگاری، الگوریتم جست و جو، هوش مصنوعی، نظریه بازی ها، پردازش چندرسانه ای، فلسفه، اقتصاد و سایر زمینه هاست. [ ۲]
ارتباط بین کلاس های پیچیدگی P و NP در نظریه پیچیدگی محاسباتی - بخشی از نظریه محاسبات که به بررسی منابع مورد نیاز در زمان محاسبه جواب یک مسئله می پردازد - مطالعه می شود. مهم ترین منابع یکی زمان ( مراحل یا گام های مورد نیاز برای دستیابی به جواب ) و دیگری فضا ( حافظه مورد نیاز برای حل مسئله ) است.

wiki: مسئله P در مقابل NP
