مرتب سازی گسترده

در علوم رایانه، مرتب سازی گسترده ( به انگلیسی: Splaysort ) یک الگوریتم مرتب سازی مقایسه ای توافقی بر مبنای ساختمان داده های درخت اسپلی است. [ ۱]
مراحل اجرای الگوریتم عبارت اند از:
• مقداردهی اولیه یک درخت اسپلی خالی صورت می گیرد؛
• برای هر آیتِم داده در ترتیب ورودی، آن را در درخت اسپلی قرار می دهد؛
• پیمایش درخت برای یافتن ترتیب داده انجام می شود.
علاوه بر این، الگوریتم با استفاده از درخت اسپلی برای سرعت بخشیدن به هر عمل درج، ممکن است به عنوان شکلی از مرتب سازی درجی یا مرتب سازی درختی هم به نظر برسد.
به عنوان مثال داده هایی با ترتیب زیر را می خواهیم مرتب کنیم:
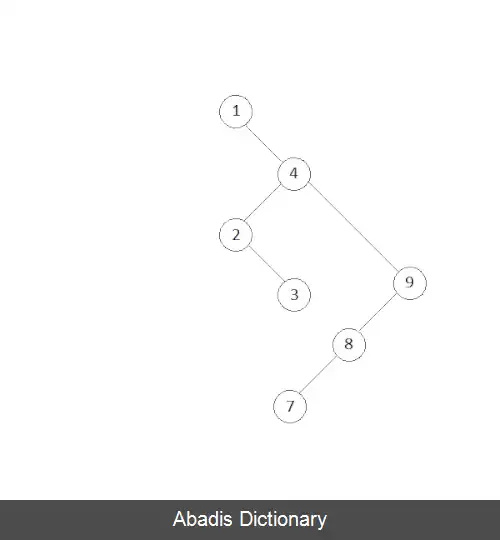
8 4 7 2 3 9 1 درج داده ها در درخت وارد کردن داده در درخت گسترده پیمایش پیش ترتیب ( In - Order ) درخت پیمایش میان ترتیب درخت ساخته شده برای آشنایی بیشتر با روش درج در این درخت به الگوریتم موجود در صفحه ی درخت گسنرده مراجعه کنید.
طبق تحلیل سرشکن، این مرتب سازی در بدترین حالت برای n داده از پیچیدگی زمانی ( O ( n  log  n است. که هم اندازه با سریع ترین الگوریتم های مرتب سازی مقایسه ای غیر توافقی مانند مرتب سازی ادغامی و مرتب سازی سریع است. برای ورودی های خاص با ترتیب به طور مثال تقریبا مرتب یا به طوری که هر عنصر با جدش در حالت مرتب فاصله ی کمی دارد، این الگوریتم می تواند بهتر از پیچیدگی زمانی ( O ( n  log  n عمل کند. این موضوع نشان می دهد این مرتب سازی یک مرتب سازی توافقی است. طبق قضیه ی Dynamic Finger [ ۲] برای درخت های اسپلی زمان اجرای این الگوریتم به شیوه ی زیر محاسبه می شود:
اگر xd را فاصله ی عنصر x از جدش و xi را برابر با اندازهٔ نابه جایی آن ( اختلاف جای x در ورودی و جای آن در داده ی مرتب سازی شده ) در نظر بگیریم، کل زمان مرتب سازی به ∑ x log ⁡ d x و ∑ x log ⁡ i x محدود می شود.
طبق محاسبات ( Moffat، Eddy و Petersson 1996 ) ، در اعداد تصادفی عامل 1. 5 تا 2، الگوریتم مرتب سازی سریع و در عامل های کوچکتر مرتب سازی ادغامی سریعتر عمل می کنند. برای داده های با مقیاس بزرگ تر، مرتب سازی سریع به دلیل الگوریتم درجا بودن کندتر است و مرتب سازی ادغامی و گسترده از نظر زمانی نزدیک به هم عمل می کنند. که اگر داده ها تقریبا مرتب باشند مرتب سازی گسترده بسیار بهتر از الگوریتم های دیگر عمل می کند. [ ۱]