الگوریتم های مرتب سازی پایدار ترتیب داده هایی که دارای کلیدهای برابر هستند را حفظ می کنند. این الگوریتم ها زمانی اهمیت پیدا میکنند که رکورد مورد مرتب سازی و کلیدی که الگوریتم برای مرتب سازی از آن استفاده می کند قابل تمایز باشند. اگر داده های با کلیدهای یکسان داشته باشیم، اگر ۲ رکورد مثلا به نام های S و R با کلیدهای یکسان داشته باشیم، و در لیست اصلی ما R قبل از S آمده باشد، در صورتی الگوریتم مرتب ساز را پایدار می گوییم که در لیست مرتب شده نیز R قبل از S بیاید.
اگر تمامی کلیدها متفاوت باشند، الگوریتم های مرتب سازی پایدار و غیرپایدار تفاوتی با هم ندارند. هنگامی که رکوردهای یکسان قابل تشخیص نباشد، مانند اعداد صحیح یا به طور عام، زمانی که داده تنها از رکورد تشکیل شده باشد، پایداری دارای اهمیت چندانی نمی باشد.
حال فرض کنید اعداد زیر برحسب رکوردهای اولشان مرتب شوند:
( ۲, ۴ ) ( ۷, ۳ ) ( ۱, ۳ ) ( ۶, ۵ ) در این مثال دو نتیجه متفاوت ممکن است رخ بدهد، اول اینکه ترتیب نسبی داده ها با رکورد یکسان حفظ شودو دیگر این که این ترتیب حفظ نشود:
( ۶, ۵ ) ( ۲, ۴ ) ( ۱, ۳ ) ( ۷, ۳ ) ( اگر ترتیب اصلی تغییر کند ) ( ۶, ۵ ) ( ۲, ۴ ) ( ۷, ۳ ) ( ۱, ۳ ) ( اگر ترتیب اصلی حفظ شود ) الگوریتم های مرتب سازی ناپایدار ترتیب نسبی عناصر با مقادیر یکسان را ممکن است تغییر دهند. اما مرتب سازی های پایدار هرگز این کار را نخواهند کرد. الگوریتم های ناپایدار به گونه ای می توانند پیاده سازی شوند تا پایداری را حفظ کنند. یک راه برای پایدار سازی این است که مقایسهٔ رکوردها را نیز اضافه کنیم، در این صورت هنگام مقایسه دو شی با رکورد یکسان تصمیم می گیریم که ترتیب اصلی عناصر را رعایت کنیم یا خیر. البته در نظر داشته باشد که این کار هزینه مرتب سازی را افزایش می دهد. مرتب سازی رکوردهای داده شده با هر الگوریتمی قابل انجام است، حال اگر مرتب سازی پایدار باشد، اگر چندین دفعه نیز آن را اجرا کنیم، جواب بدون تغییر خواهد بود.
مثال:
مرتب سازی زوج اعداد بر اساس مؤلفه اول، و سپس دوم:
( ۴ ، ۲ ) ( ۳ ، ۷ ) ( ۳ ، ۱ ) ( ۵ ، ۶ ) ( ترتیب اصلی ) ( ۳ ، ۱ ) ( ۴ ، ۲ ) ( ۵ ، ۶ ) ( ۳ ، ۷ ) ( پس مرتب سازی بر اساس مؤلفه دوم ) ( ۳ ، ۱ ) ( ۳ ، ۷ ) ( ۴ ، ۲ ) ( ۵ ، ۶ ) ( پس از مرتب سازی بر اساس مؤلفه اول ) از طرف دیگر:
( ۳ ، ۷ ) ( ۳ ، ۱ ) ( ۴ ، ۲ ) ( ۵ ، ۶ ) ( پس از مرتب سازی بر اساس مؤلفه اول ) ( ۳ ، ۱ ) ( ۴ ، ۲ ) ( ۵ ، ۶ ) ( ۳ ، ۷ ) ( پس مرتب سازی بر اساس مؤلفه دوم مرتب سازی بر اساس مؤلفه اول به هم می خورد ) الگوریتم های مرتب سازی از لحاظ پایداری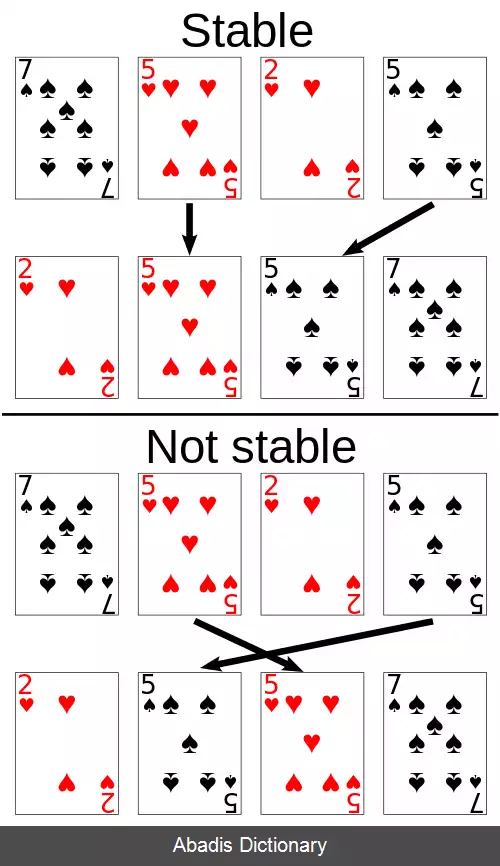

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر تمامی کلیدها متفاوت باشند، الگوریتم های مرتب سازی پایدار و غیرپایدار تفاوتی با هم ندارند. هنگامی که رکوردهای یکسان قابل تشخیص نباشد، مانند اعداد صحیح یا به طور عام، زمانی که داده تنها از رکورد تشکیل شده باشد، پایداری دارای اهمیت چندانی نمی باشد.
حال فرض کنید اعداد زیر برحسب رکوردهای اولشان مرتب شوند:
( ۲, ۴ ) ( ۷, ۳ ) ( ۱, ۳ ) ( ۶, ۵ ) در این مثال دو نتیجه متفاوت ممکن است رخ بدهد، اول اینکه ترتیب نسبی داده ها با رکورد یکسان حفظ شودو دیگر این که این ترتیب حفظ نشود:
( ۶, ۵ ) ( ۲, ۴ ) ( ۱, ۳ ) ( ۷, ۳ ) ( اگر ترتیب اصلی تغییر کند ) ( ۶, ۵ ) ( ۲, ۴ ) ( ۷, ۳ ) ( ۱, ۳ ) ( اگر ترتیب اصلی حفظ شود ) الگوریتم های مرتب سازی ناپایدار ترتیب نسبی عناصر با مقادیر یکسان را ممکن است تغییر دهند. اما مرتب سازی های پایدار هرگز این کار را نخواهند کرد. الگوریتم های ناپایدار به گونه ای می توانند پیاده سازی شوند تا پایداری را حفظ کنند. یک راه برای پایدار سازی این است که مقایسهٔ رکوردها را نیز اضافه کنیم، در این صورت هنگام مقایسه دو شی با رکورد یکسان تصمیم می گیریم که ترتیب اصلی عناصر را رعایت کنیم یا خیر. البته در نظر داشته باشد که این کار هزینه مرتب سازی را افزایش می دهد. مرتب سازی رکوردهای داده شده با هر الگوریتمی قابل انجام است، حال اگر مرتب سازی پایدار باشد، اگر چندین دفعه نیز آن را اجرا کنیم، جواب بدون تغییر خواهد بود.
مثال:
مرتب سازی زوج اعداد بر اساس مؤلفه اول، و سپس دوم:
( ۴ ، ۲ ) ( ۳ ، ۷ ) ( ۳ ، ۱ ) ( ۵ ، ۶ ) ( ترتیب اصلی ) ( ۳ ، ۱ ) ( ۴ ، ۲ ) ( ۵ ، ۶ ) ( ۳ ، ۷ ) ( پس مرتب سازی بر اساس مؤلفه دوم ) ( ۳ ، ۱ ) ( ۳ ، ۷ ) ( ۴ ، ۲ ) ( ۵ ، ۶ ) ( پس از مرتب سازی بر اساس مؤلفه اول ) از طرف دیگر:
( ۳ ، ۷ ) ( ۳ ، ۱ ) ( ۴ ، ۲ ) ( ۵ ، ۶ ) ( پس از مرتب سازی بر اساس مؤلفه اول ) ( ۳ ، ۱ ) ( ۴ ، ۲ ) ( ۵ ، ۶ ) ( ۳ ، ۷ ) ( پس مرتب سازی بر اساس مؤلفه دوم مرتب سازی بر اساس مؤلفه اول به هم می خورد ) الگوریتم های مرتب سازی از لحاظ پایداری


wiki: مرتب سازی پایدار
