مرتب سازی هرمی ( به انگلیسی: Heapsort ) ، نوعی الگوریتم است که در آن از مقایسه برای چینش یک آرایه یا فهرست استفاده می شود. این الگوریتم بخشی از خانوادهٔ مرتب سازی انتخابی است. با وجود اینکه در اکثر رایانه ها از الگوریتم چینش سریع کندتر است ولی در بدترین حالت سرعت بالاتر ( O ( n log n ) ) را دارا می باشد. این الگوریتم در محل است، ولی حالت پایداری ندارد.
در این مرتب سازی، ابتدا از کل آرایه داده شده یک درخت مکس هیپ ( یا درخت مین هیپ ) می سازد. سپس بزرگترین مقدار را برمی دارد و در انتهای آرایه مرتب شده قرار می دهد. بعد از حذف بزرگترین مقدار، دوباره از بقیه اعداد یک درخت مکس هیپ می سازد تا دومین عدد بزرگ یافت شود. بزرگ ترین مقدار در بین مقادیر باقی مانده را برمی دارد و آن را در مکان یکی قبل از انتهای آرایه قرار می دهد. این کار تا زمانی که هیچ مقداری در هرم باقی نماند و آرایه مرتب شده کامل شود، تکرار می شود.
یکی از روش های مرتب سازی داده هااست، که براساس خصوصیات درخت heap پیاده سازی شده است. بر اساس تعریف درخت heap، در یک max - heap یا min - heap بزرگترین یا کوچکترین مقدار بین داده ها همواره در ریشه درخت قرار دارد. یافتن بزرگترین یا کوچکترین عنصر بین عناصر، هزینه ثابت ( Ө ( ۱ دارد. با حذف این عنصر از درخت، بزرگترین یا کوچکترین عنصر بعدی مجدداً در ریشه قرار می گیرد. به این ترتیب با حذف متوالی عناصر درخت heap و درج آن ها در محل جدید، یک آرایه مرتب شده نزولی ویا صعودی به دست خواهد آمد.
به عنوان مثال، min - heap زیر راتوضیح می دهیم:
مراحل مرتب سازی هرمی به ترتیب زیر خواهد بود:
Step 0 ) min - heap: 1, 4, 5, 8, 6, 9 - list:
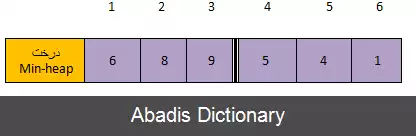
Step 1 ) min - heap: 4, 6, 5, 8, 9 - list:1
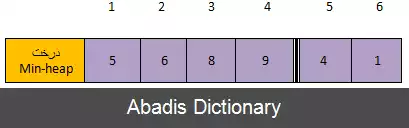
Step 2 ) min - heap: 5, 6, 9, 8 - list:1 , 4
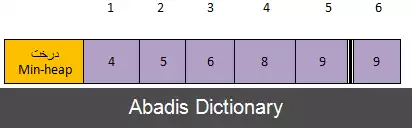
Step 3 ) min - heap: 6, 8, 9 - list:1, 4, 5
Step 4 ) min - heap: 8, 9 - list:1, 4, 5, 6
Step 5 ) min - heap: 9 - list:1, 4, 5, 6, 8
Step 6 ) min - heap: - list: 1, 4, 5, 6, 8, 9
که در آخر، آرایه list شامل اطلاعات مرتب شده صعودی است.
برای مرتب کردن عناصر با استفاده از درخت heap، نیاز به n عمل حذف گره ریشه از درخت دارد. عمل حذف گره ریشه در درخت heap خود از مرتبه ( Θ ( log n است. در نتیجه کل این عملیات از مرتبه ( Θ ( n log n خواهد بود. نکته قابل توجه دیگر، ساخت درخت heap از عناصر مورد نظر برای مرتب سازی است. در حالت عادی عناصر به صورت نامرتب و با چیدمان تصادفی در اختیار هر الگوریتم مرتب سازی قرار می گیرند. در این حالت یک هزینه زمانی دیگر برای ساخت درخت heap از روی چنین فهرستی مورد نیاز است.


این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر این مرتب سازی، ابتدا از کل آرایه داده شده یک درخت مکس هیپ ( یا درخت مین هیپ ) می سازد. سپس بزرگترین مقدار را برمی دارد و در انتهای آرایه مرتب شده قرار می دهد. بعد از حذف بزرگترین مقدار، دوباره از بقیه اعداد یک درخت مکس هیپ می سازد تا دومین عدد بزرگ یافت شود. بزرگ ترین مقدار در بین مقادیر باقی مانده را برمی دارد و آن را در مکان یکی قبل از انتهای آرایه قرار می دهد. این کار تا زمانی که هیچ مقداری در هرم باقی نماند و آرایه مرتب شده کامل شود، تکرار می شود.
یکی از روش های مرتب سازی داده هااست، که براساس خصوصیات درخت heap پیاده سازی شده است. بر اساس تعریف درخت heap، در یک max - heap یا min - heap بزرگترین یا کوچکترین مقدار بین داده ها همواره در ریشه درخت قرار دارد. یافتن بزرگترین یا کوچکترین عنصر بین عناصر، هزینه ثابت ( Ө ( ۱ دارد. با حذف این عنصر از درخت، بزرگترین یا کوچکترین عنصر بعدی مجدداً در ریشه قرار می گیرد. به این ترتیب با حذف متوالی عناصر درخت heap و درج آن ها در محل جدید، یک آرایه مرتب شده نزولی ویا صعودی به دست خواهد آمد.
به عنوان مثال، min - heap زیر راتوضیح می دهیم:
مراحل مرتب سازی هرمی به ترتیب زیر خواهد بود:
Step 0 ) min - heap: 1, 4, 5, 8, 6, 9 - list:
Step 1 ) min - heap: 4, 6, 5, 8, 9 - list:1
Step 2 ) min - heap: 5, 6, 9, 8 - list:1 , 4
Step 3 ) min - heap: 6, 8, 9 - list:1, 4, 5
Step 4 ) min - heap: 8, 9 - list:1, 4, 5, 6
Step 5 ) min - heap: 9 - list:1, 4, 5, 6, 8
Step 6 ) min - heap: - list: 1, 4, 5, 6, 8, 9
که در آخر، آرایه list شامل اطلاعات مرتب شده صعودی است.
برای مرتب کردن عناصر با استفاده از درخت heap، نیاز به n عمل حذف گره ریشه از درخت دارد. عمل حذف گره ریشه در درخت heap خود از مرتبه ( Θ ( log n است. در نتیجه کل این عملیات از مرتبه ( Θ ( n log n خواهد بود. نکته قابل توجه دیگر، ساخت درخت heap از عناصر مورد نظر برای مرتب سازی است. در حالت عادی عناصر به صورت نامرتب و با چیدمان تصادفی در اختیار هر الگوریتم مرتب سازی قرار می گیرند. در این حالت یک هزینه زمانی دیگر برای ساخت درخت heap از روی چنین فهرستی مورد نیاز است.






wiki: مرتب سازی هرمی
