مرتب سازی مسابقه ای ( به انگلیسی: Tournament sort ) یک الگوریتم مرتب سازی است. این الگوریتم مرتب سازی انتخابی ساده را با استفاده از یک صف اولویت دار یا یک درخت برنده برای پیدا کردن عنصر بعدی در مرتب سازی بهبود می بخشد. در مرتب سازی انتخابی ساده، O ( n ) عمل صورت می گیرد تا عنصر بعدی از n عنصر را انتخاب کند؛ در یک مرتب سازی مسابقه ای، O ( log n ) عمل صورت می گیرد ( پس از ساختن مسابقه ابتدایی در O ( n ) ) . مرتب سازی مسابقه ای یک تنوع از مرتب سازی هرمی است.
درخت برنده نوعی درخت مسابقه است که از n راس خارجی و n − 1 راس داخلی تشکیل می شود. رئوس خارجی نمایندهٔ بازیکنان و رئوس داخلی هر کدام نمایندهٔ یک تک مسابقه بین دو بازیکن است. در درخت برنده هر راس داخلی باید بازیکن برنده بین دو راس فرزند خود را ذخیره کند و در انتها ریشه درخت حاوی بازیکنی خواهد بود که در تمام تک مسابقه ها برنده شده است. اگر برنده را در هر تک مسابقه بازیکنی در نظر بگیریم که مقدار آن کمتر است؛ در این صورت ریشه درخت اشاره به بازیکنی خواهد داشت که کمترین مقدار را بین تمام بازیکنان دارد. با طراحی چنین داده ساختاری می توان الگوریتم مرتب سازی مسابقه ای را اجرا نمود. اگر آرایه مورد نظر برای مرتب سازی دارای k عنصر باشد؛ درخت مسابقه ای با n راس خارجی ( n اولین عدد توان ۲ است که بزرگتر یا مساوی k باشد ) و n − 1 راس داخلی می سازیم. رئوس خارجی به ترتیب به عناصر آرایه اشاره می کنند و رئوس خارجی اضافه نیز به هیچ خانه ای اشاره ندارند. رئوس داخلی درخت از پایین به بالا به برنده هر تک مسابقه اشاره می کنند تا زمانی که ریشه مشخص کنندهٔ برندهٔ نهایی شود. برندهٔ نهایی را به عنوان کوچکترین عنصر در ابتدای یک آرایهٔ جدید می گذاریم و راس خارجی که به آن اشاره داشت را از دور مسابقات حذف می کنیم. در مسیر رسیدن آن راس به ریشه مسابقات را تکرار می کنیم تا برندهٔ نهایی را با نبود راس برندهٔ دور قبل شناسایی کنیم. آن قدر به این کار ادامه می دهیم تا تمام بازیکنان از مسابقات حذف شوند. در این مرحله آرایهٔ ساخته شده مرتب خواهد بود.
زمان اجرای این الگوریتم به دو قسمت تقسیم می شود. به اندازه O ( n ) طول می کشد که بازیکنان در رئوس خارجی قرار گیرند و به اندازه O ( n ) نیز طول می کشد تا درخت برنده تکمیل شده و برندهٔ نهایی مشخص شود. سپس در هر عمل حذف بازیکن از مسابقات به اندازه O ( log n ) طول می کشد تا درخت برنده بازسازی شود. n مرتبه این عمل انجام می شود تا در نهایت آرایه مرتب شود. پس در مجموع زمان اجرای این الگوریتم از O ( n log n ) می شود. مقدار حافظه لازم برای این الگوریتم متشکل است از آرایهٔ اولیه و آرایهٔ مرتب شده و یک درخت مسابقه که تعداد رئوس خارجی آن از ۲ برابر تعداد بازیکنان کمتر است. در درخت مسابقه تعداد رئوس داخلی همیشه یکی کمتر از تعداد رئوس خارجی است. پس در کل پیچیدگی فضایی این الگوریتم از O ( n ) است.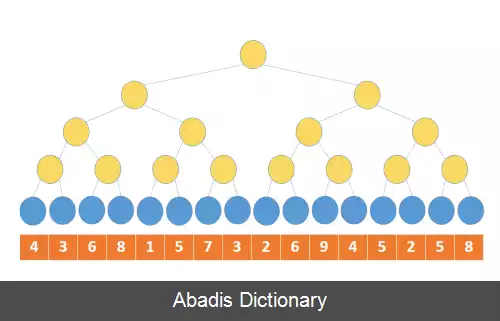

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرخت برنده نوعی درخت مسابقه است که از n راس خارجی و n − 1 راس داخلی تشکیل می شود. رئوس خارجی نمایندهٔ بازیکنان و رئوس داخلی هر کدام نمایندهٔ یک تک مسابقه بین دو بازیکن است. در درخت برنده هر راس داخلی باید بازیکن برنده بین دو راس فرزند خود را ذخیره کند و در انتها ریشه درخت حاوی بازیکنی خواهد بود که در تمام تک مسابقه ها برنده شده است. اگر برنده را در هر تک مسابقه بازیکنی در نظر بگیریم که مقدار آن کمتر است؛ در این صورت ریشه درخت اشاره به بازیکنی خواهد داشت که کمترین مقدار را بین تمام بازیکنان دارد. با طراحی چنین داده ساختاری می توان الگوریتم مرتب سازی مسابقه ای را اجرا نمود. اگر آرایه مورد نظر برای مرتب سازی دارای k عنصر باشد؛ درخت مسابقه ای با n راس خارجی ( n اولین عدد توان ۲ است که بزرگتر یا مساوی k باشد ) و n − 1 راس داخلی می سازیم. رئوس خارجی به ترتیب به عناصر آرایه اشاره می کنند و رئوس خارجی اضافه نیز به هیچ خانه ای اشاره ندارند. رئوس داخلی درخت از پایین به بالا به برنده هر تک مسابقه اشاره می کنند تا زمانی که ریشه مشخص کنندهٔ برندهٔ نهایی شود. برندهٔ نهایی را به عنوان کوچکترین عنصر در ابتدای یک آرایهٔ جدید می گذاریم و راس خارجی که به آن اشاره داشت را از دور مسابقات حذف می کنیم. در مسیر رسیدن آن راس به ریشه مسابقات را تکرار می کنیم تا برندهٔ نهایی را با نبود راس برندهٔ دور قبل شناسایی کنیم. آن قدر به این کار ادامه می دهیم تا تمام بازیکنان از مسابقات حذف شوند. در این مرحله آرایهٔ ساخته شده مرتب خواهد بود.
زمان اجرای این الگوریتم به دو قسمت تقسیم می شود. به اندازه O ( n ) طول می کشد که بازیکنان در رئوس خارجی قرار گیرند و به اندازه O ( n ) نیز طول می کشد تا درخت برنده تکمیل شده و برندهٔ نهایی مشخص شود. سپس در هر عمل حذف بازیکن از مسابقات به اندازه O ( log n ) طول می کشد تا درخت برنده بازسازی شود. n مرتبه این عمل انجام می شود تا در نهایت آرایه مرتب شود. پس در مجموع زمان اجرای این الگوریتم از O ( n log n ) می شود. مقدار حافظه لازم برای این الگوریتم متشکل است از آرایهٔ اولیه و آرایهٔ مرتب شده و یک درخت مسابقه که تعداد رئوس خارجی آن از ۲ برابر تعداد بازیکنان کمتر است. در درخت مسابقه تعداد رئوس داخلی همیشه یکی کمتر از تعداد رئوس خارجی است. پس در کل پیچیدگی فضایی این الگوریتم از O ( n ) است.


wiki: مرتب سازی مسابقه ای
