مرتب سازی شِل یا مرتب سازی صدفی یکی از قدیمی ترین الگوریتم های مرتب سازی و تعمیمی از مرتب سازی درجی با در نظر گرفتن دو نکته زیر است:
• الگوریتم مرتب سازی درجی درصورتی کارآمد است که داده ها تقریباً مرتب باشند.
• مرتب سازی درجی معمولاً کم بازده است چون مقادیر را در هر زمان فقط به اندازه یک موقعیت جابجا می کند.
مرتب سازی صدفی، الگوریتمی سریع و کارآمد و در عین حال یادگیری و پیاده سازی آن ساده است.
البته این نکته قابل توجه است که مرتب سازی صدفی درحقیقت به تنهایی داده ها را مرتب نمی کند بلکه به نوعی از سایر مرتب سازی ها استفاده کرده و با یک دسته بندی مناسب که موجب می شود تعداد دفعاتی که هر داده بررسی می شود کاهش یابد، کارایی آن ها را افزایش می دهد.
a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a 10 a 11 a 12 input data: 62 83 18 53 07 17 95 86 47 69 25 28 after 5 - sorting: 17 28 18 47 07 25 83 86 53 69 62 95 after 3 - sorting: 17 07 18 47 28 25 69 62 53 83 86 95 after 1 - sorting: 07 17 18 25 28 47 53 62 69 83 86 95
این مرتب سازی به نام مخترعش، دونالد شِل[ ۱] که این الگوریتم را در سال 1995 منتشر کرد نام گذاری شده است. برخی کتاب ها و منابع قدیمی تر این الگوریتم را «شل - مِتزنِر»[ ۲] نیز نامیده اند ولی طبق گفتهٔ خود مارلین متزنر ( Marlene Metzner ) «من هیچ کاری برای این الگوریتم انجام ندادم و اسم من هیچ وقت نباید به آن اضافه می شد» نام آن به شِل تغییر یافت.
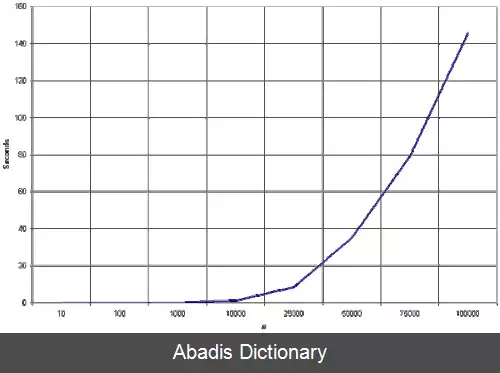
در روش مرتب سازی درجی در بدترین حالت الگوریتم از ( O ( n ۲ است درحالی که با مرتب سازی صدفی این زمان به ( O ( n log۲ کاهش یافته است.
در مرتب سازی صدفی، ابتدا داده ها در گام های بزرگتری جابه جا می شوند اما در هر مرحله فاصله این جابه جایی ها کم تر شده و به جابه جایی های جزئی می رسد.
در این الگوریتم از روش مرتب سازی درجی استفاده می شود. به عبارتی ابتدا لیست را به چند دسته تقسیم می کند و هر کدام را جداگانه مرتب می کند. برای مثال اگر در ابتدا به ۳ دسته تقسیم کند، هر دسته را جداگانه به روش درجی که گفته شد، مرتب می کند. در هر مرحله، تعداد دسته ها نصف می شود ( دسته ها بر اساس باقی مانده شان یا همان دسته های هم نهشتی ) . این عمل را ادامه می دهد تا سرانجام، تنها یک دسته شامل کل لیست داشته باشیم.
به عنوان مثال رشته f d a c b e را تحت این الگوریتم مرتب می کنیم. کد: F d a c b e: شروع

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• الگوریتم مرتب سازی درجی درصورتی کارآمد است که داده ها تقریباً مرتب باشند.
• مرتب سازی درجی معمولاً کم بازده است چون مقادیر را در هر زمان فقط به اندازه یک موقعیت جابجا می کند.
مرتب سازی صدفی، الگوریتمی سریع و کارآمد و در عین حال یادگیری و پیاده سازی آن ساده است.
البته این نکته قابل توجه است که مرتب سازی صدفی درحقیقت به تنهایی داده ها را مرتب نمی کند بلکه به نوعی از سایر مرتب سازی ها استفاده کرده و با یک دسته بندی مناسب که موجب می شود تعداد دفعاتی که هر داده بررسی می شود کاهش یابد، کارایی آن ها را افزایش می دهد.
a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a 10 a 11 a 12 input data: 62 83 18 53 07 17 95 86 47 69 25 28 after 5 - sorting: 17 28 18 47 07 25 83 86 53 69 62 95 after 3 - sorting: 17 07 18 47 28 25 69 62 53 83 86 95 after 1 - sorting: 07 17 18 25 28 47 53 62 69 83 86 95
این مرتب سازی به نام مخترعش، دونالد شِل[ ۱] که این الگوریتم را در سال 1995 منتشر کرد نام گذاری شده است. برخی کتاب ها و منابع قدیمی تر این الگوریتم را «شل - مِتزنِر»[ ۲] نیز نامیده اند ولی طبق گفتهٔ خود مارلین متزنر ( Marlene Metzner ) «من هیچ کاری برای این الگوریتم انجام ندادم و اسم من هیچ وقت نباید به آن اضافه می شد» نام آن به شِل تغییر یافت.
در روش مرتب سازی درجی در بدترین حالت الگوریتم از ( O ( n ۲ است درحالی که با مرتب سازی صدفی این زمان به ( O ( n log۲ کاهش یافته است.
در مرتب سازی صدفی، ابتدا داده ها در گام های بزرگتری جابه جا می شوند اما در هر مرحله فاصله این جابه جایی ها کم تر شده و به جابه جایی های جزئی می رسد.
در این الگوریتم از روش مرتب سازی درجی استفاده می شود. به عبارتی ابتدا لیست را به چند دسته تقسیم می کند و هر کدام را جداگانه مرتب می کند. برای مثال اگر در ابتدا به ۳ دسته تقسیم کند، هر دسته را جداگانه به روش درجی که گفته شد، مرتب می کند. در هر مرحله، تعداد دسته ها نصف می شود ( دسته ها بر اساس باقی مانده شان یا همان دسته های هم نهشتی ) . این عمل را ادامه می دهد تا سرانجام، تنها یک دسته شامل کل لیست داشته باشیم.
به عنوان مثال رشته f d a c b e را تحت این الگوریتم مرتب می کنیم. کد: F d a c b e: شروع



wiki: مرتب سازی شل
