مرتب سازی روان یک روش مرتب سازی بر پایهٔ مقایسه است. این مرتب سازی حالتی از مرتب سازی درهم است که توسط ادسخر دیکسترا در سال ۱۹۸۱ توسعه یافته است. مثل مرتب سازی درهم کران بالای مرتب سازی روان O ( n ⋅ log log n ) است. مزیت مرتب سازی روان این است که وقتی تعدادی از ورودی ها مرتب شده باشد پیچیدگی از ( O ( n شود در حالی که متوسط پیچیدگی مرتب سازی روان O ( n ⋅ log log n ) است بدون توجه به مرتب بودن یا نبودن ورودی ها
برای اینکه یک آرایه را مرتب کنیم ابتدا آن را به رشته ای از پشته ها تقسیم می کنیم که هر پشته اندازه ی مساوی یکی از اعداد فیبوناچی دارد. فرایند تقسیم ساده است - چپ ترین گرهٔ آرایه بزرگترین پشته ممکن را ایجاد می کند و بقیهٔ عناصر باقی مانده هم به همین شکل تقسیم شوند.
• هر آرایه ای با هر طول می تواند به بخش هایی با اندازه ( L ( x {\displaystyle ( L ( x} تقسیم شود توضیح: مثلاً در کوچکترین حالت L ( 0 ) = 1 {\displaystyle L ( 0 ) =1} است
• هیچ دو پشته ای طول یکسان نخواهند داشت. این رشته یک رشته با طول اکیداً نزولی از پشته ها است هم چنین یک بیت از آرایه را می توانیم برای نگه داشتن ( L ( n {\displaystyle ( L ( n} که به عنوان اندازه پشته ها استفاده می شود در نظر بگیریم. توضیح: ( L ( n {\displaystyle ( L ( n} به آرامی به سمت 2n افزایش می یابد پس در نتیجه در هر آرایه ای همیشه یک ( L ( n {\displaystyle ( L ( n} وجود دارد که از نصف اندازه آرایه بزرگتر است. برای آرایه به اندازه ۲ استثنا وجود دارداما این آرایه را می توانیم به ۲ آرایه با اندازه ۱ و 0 ( ( L ( 0 {\displaystyle ( L ( 0} و ( L ( 1 {\displaystyle ( L ( 1} ) تقسیم کنیم که هر ۲ با عدد ۱ تعریف شوند و برابر ۱ هستند.
• هیچ دو پشتهی طولی با ( L ( n {\displaystyle ( L ( n} های متوالی و پیاپی نخواهند داشت به جز دو عدد آخر که ممکن است چنین حالتی داشته باشند. اگر هیچ عنصری در چپ وجود نداشته باشد ( حتی یک تک عنصر ) بعد از بکار بردن دو ( L ( x {\displaystyle ( L ( x} و ( L ( x + 1 {\displaystyle ( L ( x+1} ( متوالی ) ما می توانیم این دو را ترکیب کنیم و عنصری بزرگتر با نام ( L ( x + 2 {\displaystyle ( L ( x+2} بسازیم و اگر ما این کار را انجام ندهیم ( ترکیب ) بعد از ( L ( x {\displaystyle ( L ( x} و ( L ( x + 1 {\displaystyle ( L ( x+1} هیچ عنصر دیگری وجود نخواهد داشت. هر پشته دارای عنصری بنام اندازه اندازه ( L ( x {\displaystyle ( L ( x} است که از چپ به راست مثل یک پشته تفاضلی سازمان دهی شده است و به ترتیب از چپ به راست دارای عنصرهای ( L ( x − 1 {\displaystyle ( L ( x - 1} و ( L ( x − 2 {\displaystyle ( L ( x - 2} ویک گرهٔ ریشه است که ابتدا برای پشته ها با طول ( L ( 0 {\displaystyle ( L ( 0} و ( L ( 1 {\displaystyle ( L ( 1} استثنا دارد ( چون ( L ( 0 {\displaystyle ( L ( 0} و ( L ( 1 {\displaystyle ( L ( 1} برابر ۱ هستند ) .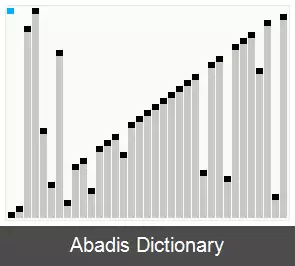

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای اینکه یک آرایه را مرتب کنیم ابتدا آن را به رشته ای از پشته ها تقسیم می کنیم که هر پشته اندازه ی مساوی یکی از اعداد فیبوناچی دارد. فرایند تقسیم ساده است - چپ ترین گرهٔ آرایه بزرگترین پشته ممکن را ایجاد می کند و بقیهٔ عناصر باقی مانده هم به همین شکل تقسیم شوند.
• هر آرایه ای با هر طول می تواند به بخش هایی با اندازه ( L ( x {\displaystyle ( L ( x} تقسیم شود توضیح: مثلاً در کوچکترین حالت L ( 0 ) = 1 {\displaystyle L ( 0 ) =1} است
• هیچ دو پشته ای طول یکسان نخواهند داشت. این رشته یک رشته با طول اکیداً نزولی از پشته ها است هم چنین یک بیت از آرایه را می توانیم برای نگه داشتن ( L ( n {\displaystyle ( L ( n} که به عنوان اندازه پشته ها استفاده می شود در نظر بگیریم. توضیح: ( L ( n {\displaystyle ( L ( n} به آرامی به سمت 2n افزایش می یابد پس در نتیجه در هر آرایه ای همیشه یک ( L ( n {\displaystyle ( L ( n} وجود دارد که از نصف اندازه آرایه بزرگتر است. برای آرایه به اندازه ۲ استثنا وجود دارداما این آرایه را می توانیم به ۲ آرایه با اندازه ۱ و 0 ( ( L ( 0 {\displaystyle ( L ( 0} و ( L ( 1 {\displaystyle ( L ( 1} ) تقسیم کنیم که هر ۲ با عدد ۱ تعریف شوند و برابر ۱ هستند.
• هیچ دو پشتهی طولی با ( L ( n {\displaystyle ( L ( n} های متوالی و پیاپی نخواهند داشت به جز دو عدد آخر که ممکن است چنین حالتی داشته باشند. اگر هیچ عنصری در چپ وجود نداشته باشد ( حتی یک تک عنصر ) بعد از بکار بردن دو ( L ( x {\displaystyle ( L ( x} و ( L ( x + 1 {\displaystyle ( L ( x+1} ( متوالی ) ما می توانیم این دو را ترکیب کنیم و عنصری بزرگتر با نام ( L ( x + 2 {\displaystyle ( L ( x+2} بسازیم و اگر ما این کار را انجام ندهیم ( ترکیب ) بعد از ( L ( x {\displaystyle ( L ( x} و ( L ( x + 1 {\displaystyle ( L ( x+1} هیچ عنصر دیگری وجود نخواهد داشت. هر پشته دارای عنصری بنام اندازه اندازه ( L ( x {\displaystyle ( L ( x} است که از چپ به راست مثل یک پشته تفاضلی سازمان دهی شده است و به ترتیب از چپ به راست دارای عنصرهای ( L ( x − 1 {\displaystyle ( L ( x - 1} و ( L ( x − 2 {\displaystyle ( L ( x - 2} ویک گرهٔ ریشه است که ابتدا برای پشته ها با طول ( L ( 0 {\displaystyle ( L ( 0} و ( L ( 1 {\displaystyle ( L ( 1} استثنا دارد ( چون ( L ( 0 {\displaystyle ( L ( 0} و ( L ( 1 {\displaystyle ( L ( 1} برابر ۱ هستند ) .


wiki: مرتب سازی روان
