مرتب سازی رتبه ای ( به انگلیسی: Rank sort ) یا مرتب سازی سرشماری ( به انگلیسی: Enumeration sort ) یک الگوریتم مرتب سازی از مرتبه ی زمانی O ( n 2 ) است که در آن برای مشخص کردن جایگاه هر عدد در لیست مرتب شده، تعداد عناصر کوچک تر از آن شمرده می شود. [ ۱]
این الگوریتم با توجّه به این که ورودی در یک داده ساختار میانی ذخیره می شود، یک نوع مرتّب سازی توزیعی است.
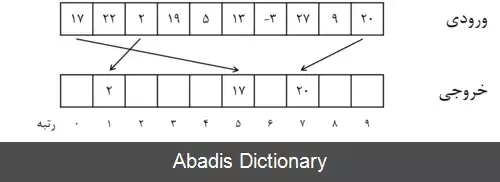
برای به دست آوردن رتبه ی هر عنصر، کافی است تعداد اعداد کوچک تر از آن را بشماریم. شکل مقابل، نمونه ای از این کار را نشان می دهد.
مرتبه ی زمانی اجرای مرتب سازی رتبه ای در تمام حالت ها O ( n 2 ) است؛ زیرا مستقل از مرتب بودن یا نبودن آرایه ی ورودی، محاسبه ی رتبه ی تمام عنصرها لازم است. با این حال، می توان با پردازش موازی زمان اجرا را بهبود داد. با استفاده از n پردازنده، می توان زمان اجرا را به O ( n ) رساند؛ در این حالت، هر پردازنده با اجرای یک حلقه، رتبه ی یک عنصر را محاسبه می کند. با وجود عملیاتی نبودن، می توان با استفاده از n 2 پردازنده زمان اجرای الگوریتم را تا O ( l g ( n ) ) هم کاهش داد. [ ۲]
قطعه کد زیر، پیاده سازی ترتیبی مرتب سازی رتبه ای را به زبان پایتون نشان می دهد. در این قطعه، آرایه ی نامرتب Input به صورت مرتب شده در آرایه ی Output ذخیره می شود.
for i in range ( n ) : rank = 0 # Number of elements less than Input for j in range ( n ) : if Input < Input: rank += 1 Output = Input # Put Input in output array based on its rank اگر لیست اولیه شامل اعداد تکراری باشد، قطعه کد بالا درست کار نمی کند؛ اما می توان با اعمال تغییراتی، این مشکل را برطرف کرد. قطعه کد زیر، نسخه ی بهبود یافته ی مرتب سازی رتبه ای را به زبان پایتون نشان می دهد.
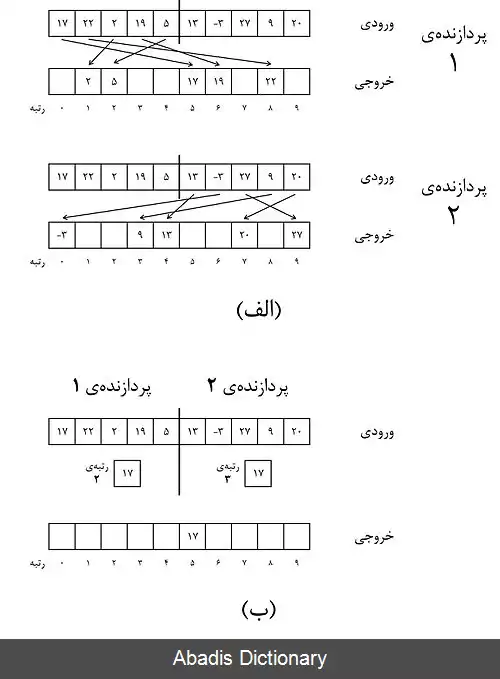
Output = * n for i in range ( n ) : rank = 0 # Number of elements less than Input for j in range ( n ) : if Input < Input: rank += 1 while Output is not None: # As long as an element has the same rank rank += 1 Output = Input # Put Input in output array based on its rank پیاده سازی موازی روش های پیاده سازی موازی مرتب سازی رتبه ای از آن جا که محاسبه کردن رتبه ی هر عنصر مستقل از عناصر دیگر است، می توان مرتب سازی رتبه ای را به صورت موازی پیاده سازی کرد. از دیدگاه تئوری، با این کار می توان زمان اجرای این الگوریتم را تا O ( 1 ) کاهش داد. برای پیاده سازی موازی روش های مختلفی وجود دارد. دو تا از این روش ها عبارت اند از:

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین الگوریتم با توجّه به این که ورودی در یک داده ساختار میانی ذخیره می شود، یک نوع مرتّب سازی توزیعی است.
برای به دست آوردن رتبه ی هر عنصر، کافی است تعداد اعداد کوچک تر از آن را بشماریم. شکل مقابل، نمونه ای از این کار را نشان می دهد.
مرتبه ی زمانی اجرای مرتب سازی رتبه ای در تمام حالت ها O ( n 2 ) است؛ زیرا مستقل از مرتب بودن یا نبودن آرایه ی ورودی، محاسبه ی رتبه ی تمام عنصرها لازم است. با این حال، می توان با پردازش موازی زمان اجرا را بهبود داد. با استفاده از n پردازنده، می توان زمان اجرا را به O ( n ) رساند؛ در این حالت، هر پردازنده با اجرای یک حلقه، رتبه ی یک عنصر را محاسبه می کند. با وجود عملیاتی نبودن، می توان با استفاده از n 2 پردازنده زمان اجرای الگوریتم را تا O ( l g ( n ) ) هم کاهش داد. [ ۲]
قطعه کد زیر، پیاده سازی ترتیبی مرتب سازی رتبه ای را به زبان پایتون نشان می دهد. در این قطعه، آرایه ی نامرتب Input به صورت مرتب شده در آرایه ی Output ذخیره می شود.
for i in range ( n ) : rank = 0 # Number of elements less than Input for j in range ( n ) : if Input < Input: rank += 1 Output = Input # Put Input in output array based on its rank اگر لیست اولیه شامل اعداد تکراری باشد، قطعه کد بالا درست کار نمی کند؛ اما می توان با اعمال تغییراتی، این مشکل را برطرف کرد. قطعه کد زیر، نسخه ی بهبود یافته ی مرتب سازی رتبه ای را به زبان پایتون نشان می دهد.
Output = * n for i in range ( n ) : rank = 0 # Number of elements less than Input for j in range ( n ) : if Input < Input: rank += 1 while Output is not None: # As long as an element has the same rank rank += 1 Output = Input # Put Input in output array based on its rank پیاده سازی موازی روش های پیاده سازی موازی مرتب سازی رتبه ای از آن جا که محاسبه کردن رتبه ی هر عنصر مستقل از عناصر دیگر است، می توان مرتب سازی رتبه ای را به صورت موازی پیاده سازی کرد. از دیدگاه تئوری، با این کار می توان زمان اجرای این الگوریتم را تا O ( 1 ) کاهش داد. برای پیاده سازی موازی روش های مختلفی وجود دارد. دو تا از این روش ها عبارت اند از:




wiki: مرتب سازی رتبه ای
