در علوم کامپیوتر، مرتب سازی جزئی حالت ساده شده ای از مسئله مرتب سازی است.
مرتب سازی عبارتست از مسئله بازگرداندن یک لیست از عناصر به طوری که عناصر آن همه مرتب شده اند، در حالی که مرتب سازی جزئی عبارتست از بازگرداند یک لیست از k تا از کوچکترین عناصر ( یا k تا از بزرگترین عناصر ) که به ترتیب قرار گرفته اند. عناصر دیگر ( عناصر بزرگتر از k تا عنصر ابتدایی ) نیز ممکن است ذخیره بشوند، یا ممکن است در نظر گرفته نشودند.
یک مثال رایج مرتب سازی جزئی محاسبه ۱۰۰ تای اول یک لیست می باشد.
در یک لیست مرتب شده جزئی، از نظر شماره خانهٔ آرایه، برای هر شماره خانه i از ۱ تا k، عنصر i ام در همان محلی که در لیست مرتب شده قرار می گیرد، قرار دارد: عنصر i از لیست مرتب شده جزئی، شامل آماره ترتیبی i از لیست ورودی است.
در مرتب سازی جزئی ما نیاز به یک لیست مرتب شده از k عنصر کوچکتر داریم. در نگاه ساده تر ما ابتدا نیاز داریم که این kعنصر را داشته باشیم، سپس آنها را مرتب کنیم. قسمت اول یعنی پیدا کردن k عنصر کوچکتر، معادل انتخاب قسمت بندی است. پس برای مرتب سازی جزئی، از این روش باید O ( n ) برای قسمت بندی و O ( k log k ) برای مرتب سازی سریع k عنصر، هزینه کنیم که در مجموع برابر O ( n + k log k ) می باشد. یک انتخاب خوب و رایج برای اجرای این الگوریتم ترکیب کردن روش های انتخاب سریع و مرتب سازی سریع می باشد که گاهی این روش را “quickselsort” نیز می نامند. [ ۱]
از داده ساختار هرم هنگامی استفاده می کنیم که k ثابت است. در این راه حل ابتدا k عنصر ابتدایی را در داخل یک هرم بیشینه می ریزیم. سپس باقی عناصر را به ترتیب داخل هرم بیشینه می ریزیم و سپس بزرگترین عنصر ( در هرم بیشینه همان راس هرم می شود ) را حذف می کنیم. در این عملیات ها برای وارد کردن هر عنصر به هرم بیشینه O ( log k ) زمان می برد که در مجموع برای n عنصر، برابر O ( n log k ) خواهد بود. این الگوریتم برای مقادیر کوچک k و مسائل برخط ( ورودی در لحظه پردازش می شود ) کاربردی خواهد بود. [ ۱]
این الگوریتم بهینه تر از الگوریتم های قبلی است. این الگوریتم بر اساس مرتب سازی سریع و مرتب سازی ادغامیمی باشد. در مرتب سازی سریع، دیگر نیازی به قسمت بازگشتی مرتب بر اساس قسمت بندی نیست. یعنی زمانی که قسمت بندی در موقعیت k یا بعد از آن قرار گیرد، ما تنها بر روی قسمت چپ بازگشتی می زنیم. [ ۲]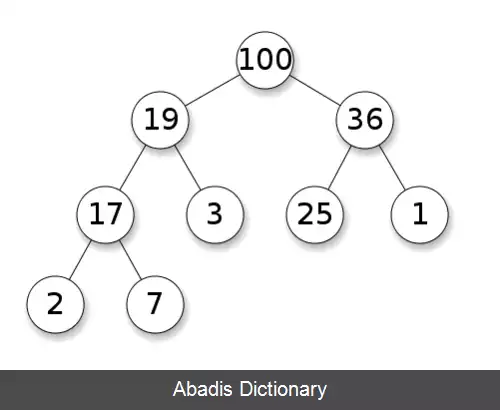
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمرتب سازی عبارتست از مسئله بازگرداندن یک لیست از عناصر به طوری که عناصر آن همه مرتب شده اند، در حالی که مرتب سازی جزئی عبارتست از بازگرداند یک لیست از k تا از کوچکترین عناصر ( یا k تا از بزرگترین عناصر ) که به ترتیب قرار گرفته اند. عناصر دیگر ( عناصر بزرگتر از k تا عنصر ابتدایی ) نیز ممکن است ذخیره بشوند، یا ممکن است در نظر گرفته نشودند.
یک مثال رایج مرتب سازی جزئی محاسبه ۱۰۰ تای اول یک لیست می باشد.
در یک لیست مرتب شده جزئی، از نظر شماره خانهٔ آرایه، برای هر شماره خانه i از ۱ تا k، عنصر i ام در همان محلی که در لیست مرتب شده قرار می گیرد، قرار دارد: عنصر i از لیست مرتب شده جزئی، شامل آماره ترتیبی i از لیست ورودی است.
در مرتب سازی جزئی ما نیاز به یک لیست مرتب شده از k عنصر کوچکتر داریم. در نگاه ساده تر ما ابتدا نیاز داریم که این kعنصر را داشته باشیم، سپس آنها را مرتب کنیم. قسمت اول یعنی پیدا کردن k عنصر کوچکتر، معادل انتخاب قسمت بندی است. پس برای مرتب سازی جزئی، از این روش باید O ( n ) برای قسمت بندی و O ( k log k ) برای مرتب سازی سریع k عنصر، هزینه کنیم که در مجموع برابر O ( n + k log k ) می باشد. یک انتخاب خوب و رایج برای اجرای این الگوریتم ترکیب کردن روش های انتخاب سریع و مرتب سازی سریع می باشد که گاهی این روش را “quickselsort” نیز می نامند. [ ۱]
از داده ساختار هرم هنگامی استفاده می کنیم که k ثابت است. در این راه حل ابتدا k عنصر ابتدایی را در داخل یک هرم بیشینه می ریزیم. سپس باقی عناصر را به ترتیب داخل هرم بیشینه می ریزیم و سپس بزرگترین عنصر ( در هرم بیشینه همان راس هرم می شود ) را حذف می کنیم. در این عملیات ها برای وارد کردن هر عنصر به هرم بیشینه O ( log k ) زمان می برد که در مجموع برای n عنصر، برابر O ( n log k ) خواهد بود. این الگوریتم برای مقادیر کوچک k و مسائل برخط ( ورودی در لحظه پردازش می شود ) کاربردی خواهد بود. [ ۱]
این الگوریتم بهینه تر از الگوریتم های قبلی است. این الگوریتم بر اساس مرتب سازی سریع و مرتب سازی ادغامیمی باشد. در مرتب سازی سریع، دیگر نیازی به قسمت بازگشتی مرتب بر اساس قسمت بندی نیست. یعنی زمانی که قسمت بندی در موقعیت k یا بعد از آن قرار گیرد، ما تنها بر روی قسمت چپ بازگشتی می زنیم. [ ۲]

wiki: مرتب سازی جزئی
