الگوریتم مرتب سازی تیم ( به انگلیسی: Timsort ) ، ترکیبی از دو الگوریتم مرتب سازی است به نام های مرتب سازی ادغامی و مرتب سازی درجی. این طراحی بر روی بسیاری از انواع داده ها در جهان واقعی بسیار خوب عمل می کند. این الگوریتم اولین بار توسط تیم پیترز ( به انگلیسی: Tim Peters ) در سال ۲۰۰۲ برای استفاده در پایتون بیان شد. الگوریتم برای پیدا کردن زیر مجموعه ای از داده ها که جستجو را بهینه تر کنند، طراحی شد. به وسیلهٔ مرتب سازی ادغامی زیر مجموعه مشخص می شود. این زیر مجموعه یک run نامیده می شود. از این runها به تعدادی پیدا می شود که معیارهای لازم برآورده شود. مرتب سازی تیم، مرتب سازی استاندارد پایتون از مدل ۲٫۳ است. هم اکنون در جاوا ۷ و همچنین در اندروید برای مرتب سازی آرایه ها از این مرتب سازی استفاده می شود. [ ۲]
الگوریتم برای استفاده از این مزیت که داده ها به طور جزئی مرتب شده اند، طراحی شده است. جستجوی تیم، کار خود را با پیداکردن runها در داده ادامه می دهد. یک run یک زیرآرایه از آرایهٔ اصلی داده ها می باشد که حداقل دارای دو عنصر می باشد که غیر نزولی یا نزولی اکید باشد. اگر زیر مجموعه نزولی باشد باید نزولی اکید باشد زیرا این run می تواند با جابجایی ساده عناصر از دو طرف که به وسط همگرا می شوند، معکوس شود.
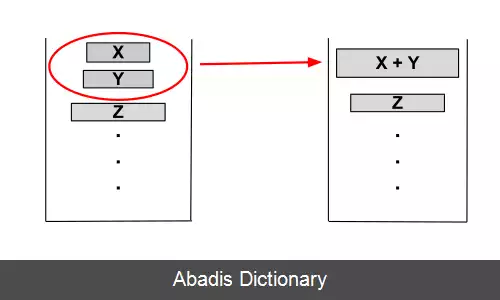
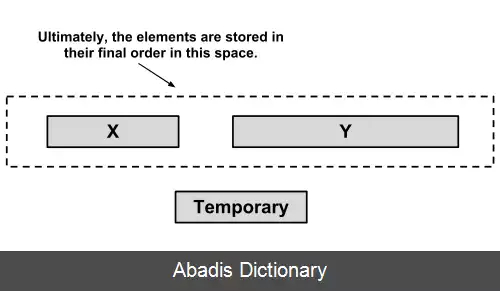
این الگوریتم اگر عناصر آن اکیداً نزولی باشد پایدار است. بعد از به دست آوردن یک run در آرایهٔ داده شده، عملیات خود را روی آن انجام می دهد و بعد از آن کار خود را با run بعدی ادامه می دهد.
یک run به طور طبیعی یک زیرآرایه است که مرتب شده است. runهای طبیعی در داده های واقعی می توانند در اندازه های مختلفی وجود داشته باشند. این الگوریتم به صورت بهینه نوع خاصی از مرتب سازی که به طول run بستگی دارد ( به طور مثال اگر اندازهٔ آن از مقدار خاصی کمتر باشد از مرتب سازی درجی استفاده می کند ) بنابراین این مرنب سازی انطباقی نامیده می شود. [ ۳] اندازهٔ run با اندازهٔ کوچکترین run مقایسه می شود. اندازهٔ کوچکترین run که «minrun» نامیده می شود که به اندازهٔ آرایه بستگی دارد. برای آرایه هایی که اندازهٔ آن از ۶۴ کمتر باشد، اندازهٔ minrun به اندازهٔ خود آرایه می باشد و اساساً به مرتب سازی درجی تبدیل می گردد. برای آرایه های بزرگتر اندازهٔ minrun بین بازهٔ ۳۲ تا ۶۵ انتخاب می شود. الگوریتم نهایی برای انتخاب minrun، شش بیت قابل توجه اندازهٔ آرایه را در نظر می گیرد. اگر هر کدام از بیت های باقی مانده یک بودند، یک اضافه می کند و از آن به عنوان minrun استفاده می کند. این روش برای همهٔ آرایه هایی که سایز آن ها از ۶۴ کمتر است و شامل یک هستند، درست عمل می کند. [ ۳]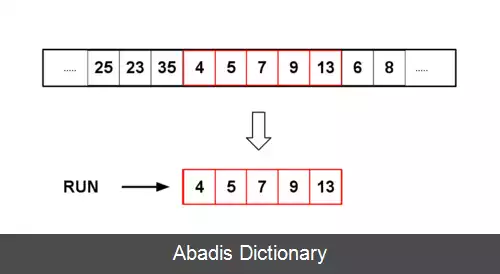

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفالگوریتم برای استفاده از این مزیت که داده ها به طور جزئی مرتب شده اند، طراحی شده است. جستجوی تیم، کار خود را با پیداکردن runها در داده ادامه می دهد. یک run یک زیرآرایه از آرایهٔ اصلی داده ها می باشد که حداقل دارای دو عنصر می باشد که غیر نزولی یا نزولی اکید باشد. اگر زیر مجموعه نزولی باشد باید نزولی اکید باشد زیرا این run می تواند با جابجایی ساده عناصر از دو طرف که به وسط همگرا می شوند، معکوس شود.
این الگوریتم اگر عناصر آن اکیداً نزولی باشد پایدار است. بعد از به دست آوردن یک run در آرایهٔ داده شده، عملیات خود را روی آن انجام می دهد و بعد از آن کار خود را با run بعدی ادامه می دهد.
یک run به طور طبیعی یک زیرآرایه است که مرتب شده است. runهای طبیعی در داده های واقعی می توانند در اندازه های مختلفی وجود داشته باشند. این الگوریتم به صورت بهینه نوع خاصی از مرتب سازی که به طول run بستگی دارد ( به طور مثال اگر اندازهٔ آن از مقدار خاصی کمتر باشد از مرتب سازی درجی استفاده می کند ) بنابراین این مرنب سازی انطباقی نامیده می شود. [ ۳] اندازهٔ run با اندازهٔ کوچکترین run مقایسه می شود. اندازهٔ کوچکترین run که «minrun» نامیده می شود که به اندازهٔ آرایه بستگی دارد. برای آرایه هایی که اندازهٔ آن از ۶۴ کمتر باشد، اندازهٔ minrun به اندازهٔ خود آرایه می باشد و اساساً به مرتب سازی درجی تبدیل می گردد. برای آرایه های بزرگتر اندازهٔ minrun بین بازهٔ ۳۲ تا ۶۵ انتخاب می شود. الگوریتم نهایی برای انتخاب minrun، شش بیت قابل توجه اندازهٔ آرایه را در نظر می گیرد. اگر هر کدام از بیت های باقی مانده یک بودند، یک اضافه می کند و از آن به عنوان minrun استفاده می کند. این روش برای همهٔ آرایه هایی که سایز آن ها از ۶۴ کمتر است و شامل یک هستند، درست عمل می کند. [ ۳]




wiki: مرتب سازی تیم
