در نظریه گرافها، یک مرتب سازی موضعی یا ترتیب موضعی یک گراف بدون دور جهت دار، یک ترتیب خطی از همه رئوس آن است به طوری که هر گره قبل از همه گره هایی می آید که از آن به آن ها یال خارج شده است. هر درخت بدون دور جهت دار یک یا چند مرتب سازی موضعی دارد. اگر گراف بدون دور نباشد آنگاه هیچ ترتیب خطی به این صورت وجود ندارد.
کاربرد اصلی مرتب سازی موضعی ( ترتیب موضعی ) در زمانبندی یک سلسله ای از کارها یا وظایف است. الگوریتم های مرتب سازی موضعی اولین بار در اوایل دهه ۱۹۶۰ در زمینه تکنیک بررسی و ارزیابی برنامه ( PERT ) برای زمانبندی در مدیریت پروژه مورد مطالعه قرار گرفت ( Jarnagin ۱۹۶۰ ) . کارها با رئوس نشان داده می شوند و یک یال از x به y وجود دارد اگر کار x باید تمام شود تا کار y بتواند شروع شود. ( برای مثال در زمان شستن لباس ها، قبل از شروع خشک شدن لباس ها، کار شستن باید تمام شود ) پس یک مرتب سازی موضعی به ما یک ترتیب برای انجام کارها می دهد.
گراف زیر، تعداد زیادی مرتب سازی موضعی قابل قبول دارد. مثل:
۷، ۵، ۳، ۱۱، ۸، ۲، ۹، ۱۰ ( چپ به راست )
۳، ۵، ۷، ۸، ۱۱، ۲، ۹، ۱۰ ( اول کم شماره ترین رأس ممکن )
۳، ۷، ۸، ۵، ۱۱، ۱۰، ۲، ۹
۵، ۷، ۳، ۸، ۱۱، ۱۰، ۹، ۲ ( اول کم ترین تعداد رأس )
۷، ۵، ۱۱، ۳، ۱۰، ۸، ۹، ۲ ( اول پرشماره ترین رأس ممکن )
۷، ۵، ۱۱، ۲، ۳، ۸، ۹، ۱۰ ( از بالا به پایین )
الگوریتم معمول مرتب سازی موضعی در زمان خطی تعداد رأس ها به اضافه تعداد یال ها یعنی ( ( O ( V+E ) اجرا می شود.
یکی از این الگوریتم ها که اولین بار توسط ( kahn ( ۱۹۶۲ شرح داده شد، با انتخاب رئوسی که در یک ترتیب احتمالی مرتب سازی موضعی هستند، کار می کند. اول یک لیست از رأس ها شروع را که هیچ یال وارد شونده ای ندارند را پیدا می کند و آن ها را در یک مجموعه می گذارد، حداقل یکی از همچنین گره هایی وجود دارد اگر گراف بدون دور باشد، سپس:
L ← Empty list that will contain the sorted elements S ← Set of all nodes with no incoming edges while S is non - empty do remove a node n from S insert n into L for each node m with an edge e from n to m do remove edge e from the graph if m has no other incoming edges then insert m into S if graph has edges then output error message ( graph has at least one cycle ) else output message ( proposed topologically sorted order: L ) اگر یک گراف، یک گراف بدون دور جهت دار باشد، لیست L حاوی یک جواب است ( جواب یکتا نیست ) . در غیر این صورت، گراف حداقل یک دور دارد پس یک مرتب سازی موضعی غیرممکن است.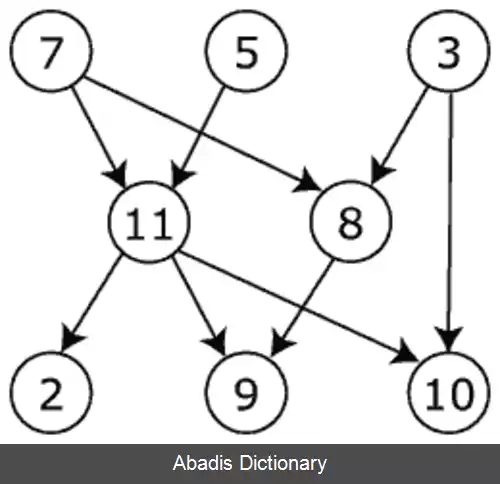

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفکاربرد اصلی مرتب سازی موضعی ( ترتیب موضعی ) در زمانبندی یک سلسله ای از کارها یا وظایف است. الگوریتم های مرتب سازی موضعی اولین بار در اوایل دهه ۱۹۶۰ در زمینه تکنیک بررسی و ارزیابی برنامه ( PERT ) برای زمانبندی در مدیریت پروژه مورد مطالعه قرار گرفت ( Jarnagin ۱۹۶۰ ) . کارها با رئوس نشان داده می شوند و یک یال از x به y وجود دارد اگر کار x باید تمام شود تا کار y بتواند شروع شود. ( برای مثال در زمان شستن لباس ها، قبل از شروع خشک شدن لباس ها، کار شستن باید تمام شود ) پس یک مرتب سازی موضعی به ما یک ترتیب برای انجام کارها می دهد.
گراف زیر، تعداد زیادی مرتب سازی موضعی قابل قبول دارد. مثل:
۷، ۵، ۳، ۱۱، ۸، ۲، ۹، ۱۰ ( چپ به راست )
۳، ۵، ۷، ۸، ۱۱، ۲، ۹، ۱۰ ( اول کم شماره ترین رأس ممکن )
۳، ۷، ۸، ۵، ۱۱، ۱۰، ۲، ۹
۵، ۷، ۳، ۸، ۱۱، ۱۰، ۹، ۲ ( اول کم ترین تعداد رأس )
۷، ۵، ۱۱، ۳، ۱۰، ۸، ۹، ۲ ( اول پرشماره ترین رأس ممکن )
۷، ۵، ۱۱، ۲، ۳، ۸، ۹، ۱۰ ( از بالا به پایین )
الگوریتم معمول مرتب سازی موضعی در زمان خطی تعداد رأس ها به اضافه تعداد یال ها یعنی ( ( O ( V+E ) اجرا می شود.
یکی از این الگوریتم ها که اولین بار توسط ( kahn ( ۱۹۶۲ شرح داده شد، با انتخاب رئوسی که در یک ترتیب احتمالی مرتب سازی موضعی هستند، کار می کند. اول یک لیست از رأس ها شروع را که هیچ یال وارد شونده ای ندارند را پیدا می کند و آن ها را در یک مجموعه می گذارد، حداقل یکی از همچنین گره هایی وجود دارد اگر گراف بدون دور باشد، سپس:
L ← Empty list that will contain the sorted elements S ← Set of all nodes with no incoming edges while S is non - empty do remove a node n from S insert n into L for each node m with an edge e from n to m do remove edge e from the graph if m has no other incoming edges then insert m into S if graph has edges then output error message ( graph has at least one cycle ) else output message ( proposed topologically sorted order: L ) اگر یک گراف، یک گراف بدون دور جهت دار باشد، لیست L حاوی یک جواب است ( جواب یکتا نیست ) . در غیر این صورت، گراف حداقل یک دور دارد پس یک مرتب سازی موضعی غیرممکن است.


wiki: مرتب سازی توپولوژیکی
