مرتب سازی ادغامی

مرتب سازی ادغام ( به انگلیسی: Merge sort ) یک الگوریتم مرتب سازی تطبیقی با زمان اجرای n log ⁡ n می باشد. در اکثر پیاده سازی ها این الگوریتم پایدار می باشد. بدین معنی که این الگوریتم ترتیب ورودی های مساوی را در خروجی مرتب شده حفظ می کند. این یک مثال از الگوریتم تقسیم و تسخیر می باشد. این الگوریتم در سال ۱۹۴۵ توسط جان فون نویمان اختراع شده است.
این روش تقریباً به صورت درختی عمل می کند و در واقع روش استفاده شده در آن روش تقسیم و حل است. الگوریتم آن در چند عمل زیر خلاصه می شود:
• گرفتن آرایه و تقسیم آن به دو زیر آرایه مساوی ( اگر طول آرایه عددی فرد باشد، طول یکی از زیر آرایه ها یک واحد بیشتر از دیگری می شود )
• بازگشت به مرحلهٔ ۱ برای هر یک از زیر آرایه ها که طول آن بزرگ تر یا مساوی ۲ است
• ادغام دو زیر آرایه
از نظر مفهومی یک الگوریتم مرتب سازی ادغام بدین صورت کار می کند:
• اگر طول لیست ۰ یا ۱ باشد آن پیش از این مرتب شده است در غیر این صورت
• لیست نامرتب را به دو زیرلیست که اندازهٔ آن ها در حدود نصف سایز لیست اولیه است، تقسیم می کند.
• هر زیرلیست را به طور بازگشتی با صدا کردن merge sort مرتب می کند.
• دو تا دوتا زیر لیست ها را از آخر ادغام می کند تا به یک لیست برسد.
مرتب سازی ادغام ۲ تا ایدهٔ اصلی را با هم ترکیب می کند تا زمان اجرایش تقویت شود.
• یک لیست کوچک از گام های کم تری برای مرتب کردن نسبت به یک لیست بزرگ استفاده می کند.
• یرای مرتب کردن دو لیست مرتب شده نسبت به دو لیست نامرتب گام های کمتری نیاز می باشد به عنوان مثال اگر این لیست ها مرتب باشند شما مجبور هستید تا هر لیست را فقط یکبار پیمایش کنید.
این الگوریتم بازگشتی ست
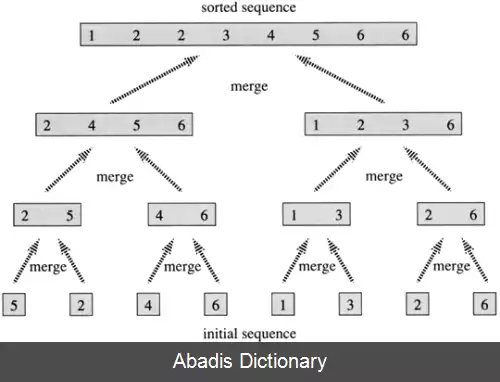
مجموعه < A=< ۵٬۲٬۴٬۶٬۱٬۳٬۲٬۶ را با استفاده از الگوریتم مرتب سازی ادغام مرتب کنید.
ابتدا این آرایه را نصف می کنیم پس دو آرایه به طول ۴ بدست می آید، که برابر است با ( ۵٬۲٬۴٬۶ ) و ( ۱٬۳٬۲٬۶ ) سپس این روال را تا جایی ادامه می دهیم که که طول آرایه هایمان برابر یک شود؛ که برابر است با: ( ۶ ) ( ۲ ) ( ۳ ) ( ۱ ) ( 6 ) ( ۴ ) ( ۲ ) ( ۵ ) حال به صورت زیر آن ها را با هم ادغام می کنیم تا به آرایه اصلی مان برسیم.
در مرتب کردن n تا عنصر مرتب سازی ادغام در حالت میانگین و بدترین حالت دارای زمان اجرای n l g n می باشد. اگر زمان اجرای مرتب سازی ادغام برای یک لیست به طول T ( n ) , n باشد بنابراین رابطهٔ بازگشتی T ( n ) = 2 T ( n / 2 ) + n از تعریف الگوریتم پیروی می کند. در این الگوریتم هر دفعه لیست را به دو زیرلیست تقسیم می کنیم و در هر مرحله n تا گام برای ادغام کردن لازم می باشد.