در علوم رایانه، مرتب سازی ادغام - درج یا الگوریتم فورد - جانسون از الگوریتم های مرتب سازی مقایسه ای است که در سال ۱۹۵۹ توسط لستر رادولف فورد و سلمر مارتین جانسون منتشر شد. این الگوریتم از الگوریتم های شناخته شده قبلی همچون مرتب سازی درجی دودویی و مرتب سازی ادغامی در بدترین حالت، از تعداد مقایسه های کمتری استفاده می کند.
مشخص است که کم بودن تعداد مقایسه ها معیاری مناسب برای اثربخشی یک الگوریتم مرتب سازی نیست؛ امّا از دیدگاه نظری کمینه کردن تعداد مقایسه ها در مسائل مرتب سازی همواره مهم بوده است. [ ۱] همین الگوریتم توسط ریاضیدان لهستانی به طور مستقل کشف شد.
فرض می کنیم ۵ عدد داریم ( a , b , c , d , e ) ، آن ها را به سه دسته تقسیم می کنیم: ( a , b ) ( c , d ) ( e )
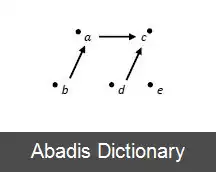
سپس دو عدد موجود در دسته های دوتایی را باهم مقایسه می کنیم و بعد از آن دو عدد بزرگتر هر دسته را با یکدیگر مقایسه می کنیم. فرض می کنیم a > b , c > d . آنگاه باید دو عدد a , c را با هم مقایسه کنیم. در شکل های زیر جهت پیکان از عدد کوچکتر به سمت عدد بزرگتر است.
با توجه به شکل بالا داریم b < a < c . اکنون باید عنصر e را بین این سه عنصر مرتب شده درج کنیم که با دو مقایسه امکان پذیر است. ( مرتب سازی درجی دودویی ) سپس بعد از معلوم شدن جایگاه e ، عنصر d را در صف مرتب شده درج می کنیم که آن نیز با دو مقایسه امکان پذیر است.
الگوریتم فورد - جانسون یا مرتب سازی ادغام - درج تعمیم جالبی از مقدمه بالاست. مراحل این الگوریتم به شرح زیر است:[ ۱] [ ۲] [ ۳]
• n {\displaystyle n} عنصر موجود را به ⌊ n 2 ⌋ {\displaystyle \left\lfloor {\frac {n}{2}}\right\rfloor } گروه دوتایی تقسیم می کنیم؛ و اگر n {\displaystyle n} فرد بود، یک عنصر جفت نشده باقی می ماند.
• ⌊ n 2 ⌋ {\displaystyle \left\lfloor {\frac {n}{2}}\right\rfloor } مقایسه انجام می دهیم تا عنصر بزرگتر در هر گروه را بیابیم.
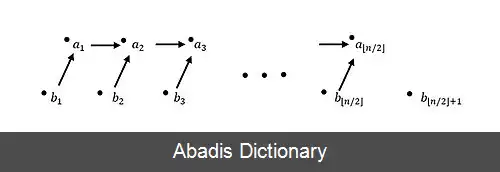
• ⌊ n 2 ⌋ {\displaystyle \left\lfloor {\frac {n}{2}}\right\rfloor } عنصر بزرگتر را به شکل بازگشتی مرتب می کنیم. حال عناصر مرتب شده را زنجیره اصلی می نامیم که به صورت a i {\displaystyle a_{i}} در شکل نمایش داده شده است.
• سپس با توجه به این که زنجیره اصلی مرتب شده است و عنصر a 1 {\displaystyle a_{1}} کوچکترین عنصر زنجیره است و می دانیم b 1 {\displaystyle b_{1}} از آن کوچکتر است، بنابراین می توان b 1 {\displaystyle b_{1}} را در ابتدای زنجیره درج نمود.
• بقیه عناصر که به شکل b i {\displaystyle b_{i}} نشان داده شده است را در زنجیره اصلی درج می کنیم. ( با استفاده از مرتب سازی درجی )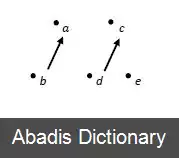
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمشخص است که کم بودن تعداد مقایسه ها معیاری مناسب برای اثربخشی یک الگوریتم مرتب سازی نیست؛ امّا از دیدگاه نظری کمینه کردن تعداد مقایسه ها در مسائل مرتب سازی همواره مهم بوده است. [ ۱] همین الگوریتم توسط ریاضیدان لهستانی به طور مستقل کشف شد.
فرض می کنیم ۵ عدد داریم ( a , b , c , d , e ) ، آن ها را به سه دسته تقسیم می کنیم: ( a , b ) ( c , d ) ( e )
سپس دو عدد موجود در دسته های دوتایی را باهم مقایسه می کنیم و بعد از آن دو عدد بزرگتر هر دسته را با یکدیگر مقایسه می کنیم. فرض می کنیم a > b , c > d . آنگاه باید دو عدد a , c را با هم مقایسه کنیم. در شکل های زیر جهت پیکان از عدد کوچکتر به سمت عدد بزرگتر است.
با توجه به شکل بالا داریم b < a < c . اکنون باید عنصر e را بین این سه عنصر مرتب شده درج کنیم که با دو مقایسه امکان پذیر است. ( مرتب سازی درجی دودویی ) سپس بعد از معلوم شدن جایگاه e ، عنصر d را در صف مرتب شده درج می کنیم که آن نیز با دو مقایسه امکان پذیر است.
الگوریتم فورد - جانسون یا مرتب سازی ادغام - درج تعمیم جالبی از مقدمه بالاست. مراحل این الگوریتم به شرح زیر است:[ ۱] [ ۲] [ ۳]
• n {\displaystyle n} عنصر موجود را به ⌊ n 2 ⌋ {\displaystyle \left\lfloor {\frac {n}{2}}\right\rfloor } گروه دوتایی تقسیم می کنیم؛ و اگر n {\displaystyle n} فرد بود، یک عنصر جفت نشده باقی می ماند.
• ⌊ n 2 ⌋ {\displaystyle \left\lfloor {\frac {n}{2}}\right\rfloor } مقایسه انجام می دهیم تا عنصر بزرگتر در هر گروه را بیابیم.
• ⌊ n 2 ⌋ {\displaystyle \left\lfloor {\frac {n}{2}}\right\rfloor } عنصر بزرگتر را به شکل بازگشتی مرتب می کنیم. حال عناصر مرتب شده را زنجیره اصلی می نامیم که به صورت a i {\displaystyle a_{i}} در شکل نمایش داده شده است.
• سپس با توجه به این که زنجیره اصلی مرتب شده است و عنصر a 1 {\displaystyle a_{1}} کوچکترین عنصر زنجیره است و می دانیم b 1 {\displaystyle b_{1}} از آن کوچکتر است، بنابراین می توان b 1 {\displaystyle b_{1}} را در ابتدای زنجیره درج نمود.
• بقیه عناصر که به شکل b i {\displaystyle b_{i}} نشان داده شده است را در زنجیره اصلی درج می کنیم. ( با استفاده از مرتب سازی درجی )



wiki: مرتب سازی ادغام درج
