مدل پولی هدرال - که به آن روش پولی توپ نیز گفته می شود - یک چهارچوب ریاضی برای اجرای تعداد بالای عملیات است. این تعداد باید به اندازه ای زیاد باشد که نتوان آن را صراحتاً عددگذاری کرد و در نتیجه یک نمایش فشرده لازم داشته باشد. برنامه های شامل حلقه های تو در تو تنها یکی از مثال های معمول این روش هستند. هم چنین متداول ترین کاربرد این مدل برای بهینه سازی حلقه های تو در تو، در برنامه ی بهینه سازی است. روش پولی هدرال با هر تکرار حلقه، در حلقه های تو در تو به عنوان نقاط مشبک داخل اشیای ریاضی به نام پولی هدرا، تبدیلات آفینی یا به صورت عمومی تر تبدیلات غیرآفینی مانند کاشی کاری را روی پولی هدرا اعمال می کند. سپس این پولی توپ های تبدیل شده را از طریق پویش پولی هدرا به شکل حلقه های تو در توی معادل، اما بهینه ( وابسته به هدف بهینه سازی تعیین شده ) در می آورد.
مثال زیر که با زبان C برنامه نویسی شده است را ملاجظه کنید.
const int n = 100; int i, j, a; for ( i = 1; i < n; i++ ) { for ( j = 1; j < ( i + 2 ) & & j < n; j++ ) { a = a + a; } } مسأله ی اصلی این کد در این است که در هر تکرار حلقه ی داخلی، محاسبه ی [a[j به نتیجه ی [a[j - 1 در تکرار قبلی حلقه وابسته است. نتیجتاً این کد به همان صورتی که هست قابل موازی سازی یا پایپ لاین شدن نیست.
یکی از کاربردهای مدل پولی توپ با استفاده از تبدیل آفینی ( i ′ , j ′ ) = ( i + j , j ) و ایجاد تغییرات مناسب در مرزها این است که حلقه های تو در توی کد بالا را به:
a = a + a; تبدیل می کند. در این حالت، هیچ یک از تکرارهای حلقه ی داخلی وابسته به نتیجه ی تکرار قیبس نیست. در نتیجه کل حلقه ی داخلی می تواند به صورت موازی اجرا شود. ( با این وجود، هر تکرار حلقه ی خارجی وابسته به تکرار قبلی است. )
کد C ذیل، نوعی از تفکیک توزیع خطا مشابه با تفکیک فلوید - اشتاینبرگ است که به دلایل آموزشی تغییر داده شده است. آرایه ی دو بعدی src شامل h ردیف است که هر یک w پیکسل دارند. هر کدام از این پیکسل ها شامل یک مقدار بین صفر تا ۲۵۵ در مقیاس خاکستری است. بعد از پایان روتین آرایه ی خروجی dst شامل پیکسل هایی است که یا مقدار صفر دارند و یا ۲۵۵. در حین اجرای محاسبات، تفکیک خطای هر پیکسل با دوباره اضافه شدن به آرایه ی src جمع آوری شده است. ( به این نکته دقت کنید که در طی محاسبات، هر دو آرایه ی src و dst هم زمان نوشته و خوانده می شوند. src فقط قابل خواندن نیست و dst هم فقط قابل نوشتن نیست. )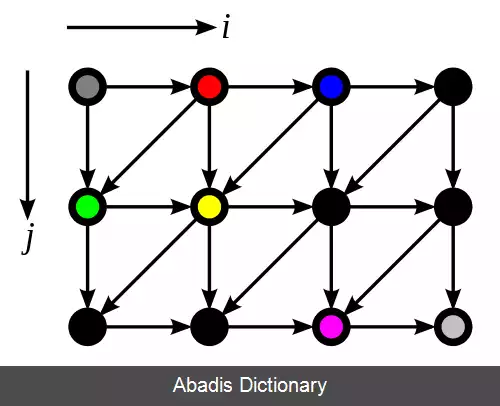
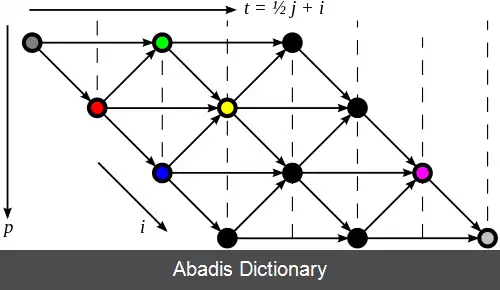
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمثال زیر که با زبان C برنامه نویسی شده است را ملاجظه کنید.
const int n = 100; int i, j, a; for ( i = 1; i < n; i++ ) { for ( j = 1; j < ( i + 2 ) & & j < n; j++ ) { a = a + a; } } مسأله ی اصلی این کد در این است که در هر تکرار حلقه ی داخلی، محاسبه ی [a[j به نتیجه ی [a[j - 1 در تکرار قبلی حلقه وابسته است. نتیجتاً این کد به همان صورتی که هست قابل موازی سازی یا پایپ لاین شدن نیست.
یکی از کاربردهای مدل پولی توپ با استفاده از تبدیل آفینی ( i ′ , j ′ ) = ( i + j , j ) و ایجاد تغییرات مناسب در مرزها این است که حلقه های تو در توی کد بالا را به:
a = a + a; تبدیل می کند. در این حالت، هیچ یک از تکرارهای حلقه ی داخلی وابسته به نتیجه ی تکرار قیبس نیست. در نتیجه کل حلقه ی داخلی می تواند به صورت موازی اجرا شود. ( با این وجود، هر تکرار حلقه ی خارجی وابسته به تکرار قبلی است. )
کد C ذیل، نوعی از تفکیک توزیع خطا مشابه با تفکیک فلوید - اشتاینبرگ است که به دلایل آموزشی تغییر داده شده است. آرایه ی دو بعدی src شامل h ردیف است که هر یک w پیکسل دارند. هر کدام از این پیکسل ها شامل یک مقدار بین صفر تا ۲۵۵ در مقیاس خاکستری است. بعد از پایان روتین آرایه ی خروجی dst شامل پیکسل هایی است که یا مقدار صفر دارند و یا ۲۵۵. در حین اجرای محاسبات، تفکیک خطای هر پیکسل با دوباره اضافه شدن به آرایه ی src جمع آوری شده است. ( به این نکته دقت کنید که در طی محاسبات، هر دو آرایه ی src و dst هم زمان نوشته و خوانده می شوند. src فقط قابل خواندن نیست و dst هم فقط قابل نوشتن نیست. )


wiki: مدل پولی توپ
