در ریاضیات مالی، مدل واسیچک ( به انگلیسی: vasicek model ) یک مدل ریاضی برای توصیف تکامل نرخ بهره است. این نوع از مدل، نرخ کوتاه مدت تک عاملی است که تغییرات نرخ بهره را با توجه به یک نوع از ریسک بازار توصیف می کند. این مدل می تواند در ارزیابی نرخ بهره اوراق مشتقه استفاده شود؛ و نیز با بازارهای اعتباری تطابق داده شده است، گرچه استفاده از آن در بازارهای اعتباری اشتباه است و به احتمالات منفی اشاره می کند. اما آن در سال ۱۹۷۷ توسط 《Oldřich Vašíček 》معروف شد[ ۱] و توانست به عنوان مدل سرمایه گذاری شناخته شود.
این مدل نشان می دهد که نرخ بهره آنی پیرو معادله دیفرانسیل تصادفی می باشد.
که wt فرایند وینر تحت ریسک مستقل از چارچوب مدل سازی در عامل ریسک بازار به صورت تصادفی است، چرا که جریان مستمر اعداد تصادفی در سیستم را مدل سازی می کند. پارامتر انحراف استاندارد σ، نوسانات نرخ بهره را تعیین می کند و تا اندازه ای نوسانات جریان تصادفی آنی را مشخص می کند. پارامترهای نوع a ، b وσ همراه با شرایط اولیه ro، به طور کامل دینامیک را مشخص می کند، و با غیرمنفی فرض کردن a، به صورت زیر مشخص می شود b :"میانگین میزان بلند مدت": تمام منحنی های بعدی r پیرامون میانگین میزان b در درازمدت خواهد بود. a:" سرعت بازگشت":a سرعتی را مشخص می کند که در آن منحنی ها پیرامون b جمع می گردند. σ: "نوسانات آنی ( لحظه ای ) "، دامنهٔ اعداد تصادفی ورودی به سیستم را لحظه به لحظه اندازه گیری می کند. هر چه σ بیشتر باشد اعداد تصادفی بیشتر خواهد بود. مقدار مشتق شدهٔ زیر نیز مورد توجه است
• σ 2 / ( 2 a ) {\displaystyle {\sigma ^{2}}/ ( 2a ) } : واریانس بلند مدت: تمام منحنی های بعدیِ r اطراف میانگین بلند مدت با چنین واریانسی در طول زمان جمع خواهند شد.
aوσ مخالف یکدیگرند: افزایش σ، میزان اعداد تصادفی ورودی به سیستم را افزایش می دهد، اما در عین حال افزایش a باعث افزایش سرعت می شود که در آن سیستم به صورت آماری در میانگین بلند مدت با واریانسِ تعیین شده توسط a، ثابت خواهد شد؛ که با مشاهدهٔ واریانس بلند مدت این موضوع روشن خواهد شد.
که در آن افزایش با σ، وکاهش با a می باشد. این یک مدل فرایند تصادفی از Ornstein–Uhlenbeck است. ایجاد میانگین تصادفی در SDE، یک نسخهٔ ساده شده از cointelation SDE است[ ۲] .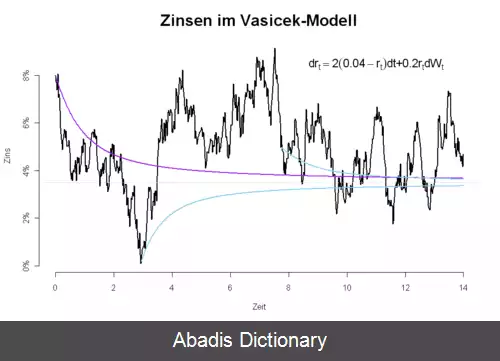
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین مدل نشان می دهد که نرخ بهره آنی پیرو معادله دیفرانسیل تصادفی می باشد.
که wt فرایند وینر تحت ریسک مستقل از چارچوب مدل سازی در عامل ریسک بازار به صورت تصادفی است، چرا که جریان مستمر اعداد تصادفی در سیستم را مدل سازی می کند. پارامتر انحراف استاندارد σ، نوسانات نرخ بهره را تعیین می کند و تا اندازه ای نوسانات جریان تصادفی آنی را مشخص می کند. پارامترهای نوع a ، b وσ همراه با شرایط اولیه ro، به طور کامل دینامیک را مشخص می کند، و با غیرمنفی فرض کردن a، به صورت زیر مشخص می شود b :"میانگین میزان بلند مدت": تمام منحنی های بعدی r پیرامون میانگین میزان b در درازمدت خواهد بود. a:" سرعت بازگشت":a سرعتی را مشخص می کند که در آن منحنی ها پیرامون b جمع می گردند. σ: "نوسانات آنی ( لحظه ای ) "، دامنهٔ اعداد تصادفی ورودی به سیستم را لحظه به لحظه اندازه گیری می کند. هر چه σ بیشتر باشد اعداد تصادفی بیشتر خواهد بود. مقدار مشتق شدهٔ زیر نیز مورد توجه است
• σ 2 / ( 2 a ) {\displaystyle {\sigma ^{2}}/ ( 2a ) } : واریانس بلند مدت: تمام منحنی های بعدیِ r اطراف میانگین بلند مدت با چنین واریانسی در طول زمان جمع خواهند شد.
aوσ مخالف یکدیگرند: افزایش σ، میزان اعداد تصادفی ورودی به سیستم را افزایش می دهد، اما در عین حال افزایش a باعث افزایش سرعت می شود که در آن سیستم به صورت آماری در میانگین بلند مدت با واریانسِ تعیین شده توسط a، ثابت خواهد شد؛ که با مشاهدهٔ واریانس بلند مدت این موضوع روشن خواهد شد.
که در آن افزایش با σ، وکاهش با a می باشد. این یک مدل فرایند تصادفی از Ornstein–Uhlenbeck است. ایجاد میانگین تصادفی در SDE، یک نسخهٔ ساده شده از cointelation SDE است[ ۲] .

wiki: مدل واسیچک
