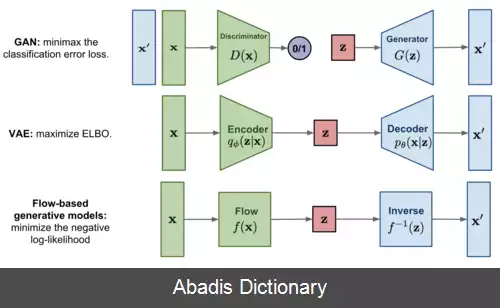
مدل سازنده مبتنی بر جریان نوعی مدل سازنده است که در یادگیری ماشین استفاده می شود که یک توزیع احتمال را با اعمال جریان نرمال سازی[ ۱] مدل می کند. این یک روش آماری با استفاده از قانون تغییر متغیر احتمالات برای تبدیل یک توزیع ساده به یک توزیع پیچیده است. مدل سازی مستقیم احتمال مزایای بسیاری دارد و نمونه های جدید را می توان با نمونه برداری از توزیع اولیه و اعمال تبدیل جریان تولید کرد. در مقابل مدل سازنده مبتنی بر جریان، بسیاری از روش های مدل سازی سازنده جایگزین مانند خودرمزگذار متغیر ( VAE ) و شبکه های سازنده تخاصمی تابع احتمال را نشان نمی دهند.
این روش شبیه به خودرمزگذار متغیر است با این تفاوت که به جای استفاده از رمزگذار و رمزگشا از یک جریان معکوس پذیر استفاده می شود. به این صورت که به جای رمزگذاری، جریان، ورودی را به فضای داده انتقال می دهد و سپس معکوس جریان، خروجی را تولید می کند. هدف این است که خروجی و ورودی کمترین تفاوت را با یکدیگر داشته باشند. پس از یادگیری به این روش، مدل باید قادر باشد تا با گرفتن یک بردار ویژگی از فضا و استفاده از معکوس جریان، خروجی معقولی تولید کند.
انواع مختلفی از این مدل ها وجود دارد. در اینجا به توضیح دو مورد از مهم ترین نمونه ها می پردازیم.
• Real Non - Volume Preserving ( Real NVP ) :[ ۲]
این مدل کلی شده نوع دیگری از مدل های مبتنی بر جریان به نام NICE است. روابط آن به صورت زیر می باشد:
x = = f θ ( z ) = +
معکوس آن z 1 = x 1 , z 2 = e − s θ ( x 1 ) ⊙ ( x 2 − m θ ( x 1 ) ) و ژاکوبین آن ∏ i = 1 n e s θ ( z 1 , ) است. که z در آن خروجی جریان و m θ هر شبکه عصبی با وزن های θ است.
نقشه Real NVP نیمه اول و دوم بردار x را جدا نگه می دارد، معمولاً باید بعد از هر لایه Real NVP یک جایگشت به صورت ( x 1 , x 2 ) ↦ ( x 2 , x 1 ) اضافه شود.
• Generative Flow ( Glow ) ( جریان سازنده ) :[ ۳]
در این مدل، هر لایه ۳ قسمت دارد.
• تبدیل وابسته به کانال با فرمول y c i j = s c ( x c i j + b c ) {\displaystyle y_{cij}=s_{c} ( x_{cij}+b_{c} ) }
و ژاکوبین ∏ c s c H W
• کانولوشن 1x1 معکوس پذیر با فرمول
z c i j = ∑ c ′ K c c ′ y c i j با ژاکوبین det ( K ) H W است که K هر ماتریس دلخواه معکوس پذیر است. Real NVP که بالاتر توضیح داده شد. علت استفاده از لایه کانولوشن معکوس پذیر 1x1 استفاده از جایگشت همه لایه هاست. ( برخلاف Real NVP که تنها از جایگشت نیمه های اول و دوم استفاده می کند )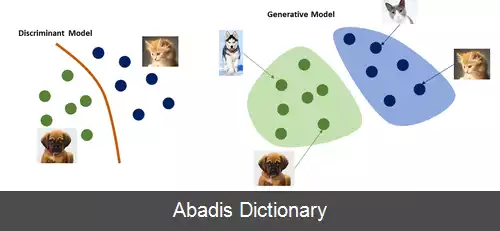
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین روش شبیه به خودرمزگذار متغیر است با این تفاوت که به جای استفاده از رمزگذار و رمزگشا از یک جریان معکوس پذیر استفاده می شود. به این صورت که به جای رمزگذاری، جریان، ورودی را به فضای داده انتقال می دهد و سپس معکوس جریان، خروجی را تولید می کند. هدف این است که خروجی و ورودی کمترین تفاوت را با یکدیگر داشته باشند. پس از یادگیری به این روش، مدل باید قادر باشد تا با گرفتن یک بردار ویژگی از فضا و استفاده از معکوس جریان، خروجی معقولی تولید کند.
انواع مختلفی از این مدل ها وجود دارد. در اینجا به توضیح دو مورد از مهم ترین نمونه ها می پردازیم.
• Real Non - Volume Preserving ( Real NVP ) :[ ۲]
این مدل کلی شده نوع دیگری از مدل های مبتنی بر جریان به نام NICE است. روابط آن به صورت زیر می باشد:
x = = f θ ( z ) = +
معکوس آن z 1 = x 1 , z 2 = e − s θ ( x 1 ) ⊙ ( x 2 − m θ ( x 1 ) ) و ژاکوبین آن ∏ i = 1 n e s θ ( z 1 , ) است. که z در آن خروجی جریان و m θ هر شبکه عصبی با وزن های θ است.
نقشه Real NVP نیمه اول و دوم بردار x را جدا نگه می دارد، معمولاً باید بعد از هر لایه Real NVP یک جایگشت به صورت ( x 1 , x 2 ) ↦ ( x 2 , x 1 ) اضافه شود.
• Generative Flow ( Glow ) ( جریان سازنده ) :[ ۳]
در این مدل، هر لایه ۳ قسمت دارد.
• تبدیل وابسته به کانال با فرمول y c i j = s c ( x c i j + b c ) {\displaystyle y_{cij}=s_{c} ( x_{cij}+b_{c} ) }
و ژاکوبین ∏ c s c H W
• کانولوشن 1x1 معکوس پذیر با فرمول
z c i j = ∑ c ′ K c c ′ y c i j با ژاکوبین det ( K ) H W است که K هر ماتریس دلخواه معکوس پذیر است. Real NVP که بالاتر توضیح داده شد. علت استفاده از لایه کانولوشن معکوس پذیر 1x1 استفاده از جایگشت همه لایه هاست. ( برخلاف Real NVP که تنها از جایگشت نیمه های اول و دوم استفاده می کند )


