مدل پنهان مارکوف ( به انگلیسی: Hidden Markov Model ) یک مدل مارکوف آماری است که در آن سیستم مدل شده به صورت یک فرایند مارکوف با حالت های مشاهده نشده ( پنهان ) فرض می شود. یک مدل پنهان مارکوف می تواند به عنوان ساده ترین شبکه بیزی پویا در نظر گرفته شود.
در مدل عادی مارکوف، حالت به طور مستقیم توسط ناظر قابل مشاهده است و بنابراین احتمال های انتقال بین حالت ها تنها پارامترهای موجود است. در یک مدل پنهان مارکوف، حالت به طور مستقیم قابل مشاهده نیست، اما خروجی، بسته به حالت، قابل مشاهده است. هر حالت یک توزیع احتمال روی سمبل های خروجی ممکن دارد؛ بنابراین دنبالهٔ سمبل های تولید شده توسط یک مدل پنهان مارکوف اطلاعاتی دربارهٔ دنبالهٔ حالت ها می دهد. توجه داشته باشید که صفت 'پنهان' به دنبالهٔ حالت هایی که مدل از آن ها عبور می کند اشاره دارد، نه به پارامترهای مدل؛ حتی اگر پارامترهای مدل به طور دقیق مشخص باشند، مدل همچنان 'پنهان' است.
مدل های پنهان مارکوف بیشتر به دلیل کاربردشان در بازشناخت الگو، مانند تشخیص صدا و دست خط، تشخیص اشاره و حرکت، برچسب گذاری اجزای سخن، بیوانفورماتیک و … شناخته شده هستند.
مدل پنهان مارکوف در حالت گسسته جز خانوادهٔ مسائل ظرف ها قرار می گیرد. به طور مثال از ربینر ۱۹۸۹: ظروف x1، x2، x3. . . و توپهای رنگی y1, y2, y3… را در نظر می گیریم، که نفر مقابل دنباله ای از توپ ها را مشاهده کرده ولی اطلاعی از دنبالهٔ ظرف هایی که توپ ها از آن ها انتخاب شده ندارد. ظرف n ام با احتمالی وابسته به ظرف n - 1 ام انتخاب می شود و چون به انتخاب ظرف های خیلی قبل تر وابسته نیست یک فرایند مارکوف است.
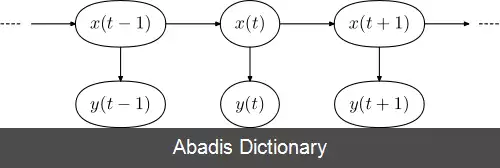
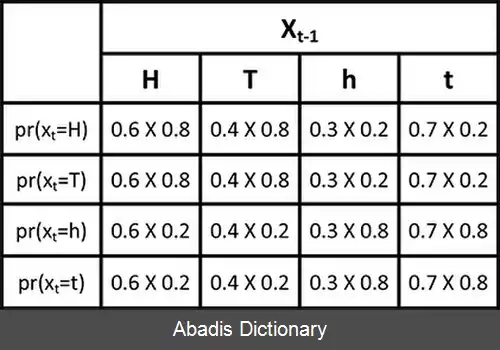
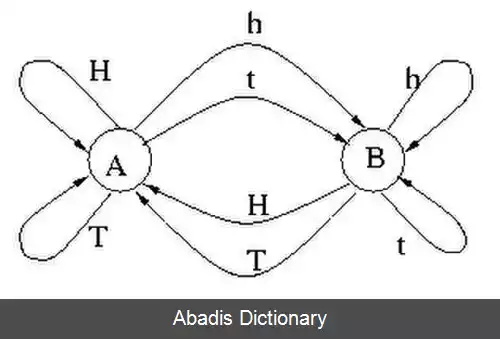
شکل زیر معماری کلی یک نمونه HMM را نشان می دهد. هر شکل بیضی یک متغیر تصادفی است که می تواند هر عددی از مقادیر را انتخاب کند. متغیر تصادفی x ( t ) یک حالت پنهان در زمان t و متغیر تصادفی y ( t ) مشاهده در زمان t است. فلش ها به معنای وابستگی های شرطی می باشند. از شکل مشخص است که توزیع احتمال شرطی متغیر پنهان x ( t ) ، در همهٔ زمان هایt مقداری را برایx ارائه می دهد که فقط به مقدار متغیر پنهان x ( t − 1 ) وابسته است: مقادیر در زمان های t - 2 و قبل تر از آن هیچ اثری ندارند. این مشخصهٔ مارکف نامیده می شود. به طور مشابه، مقدار متغیر مشاهده ای y ( t ) تنها به مقدار متغیر پنهان x ( t ) ( هر دو در زمان خاص t ) بستگی دارد. در حالت استاندارد مدل پنهان مارکوف که در اینجا در نظر گرفته شده است، فضای حالت متغیرهای پنهان گسسته است؛ درحالی که متغیرهای مشاهده ای می توانند گسسته یا پیوسته ( از توزیع گوسین ) باشند.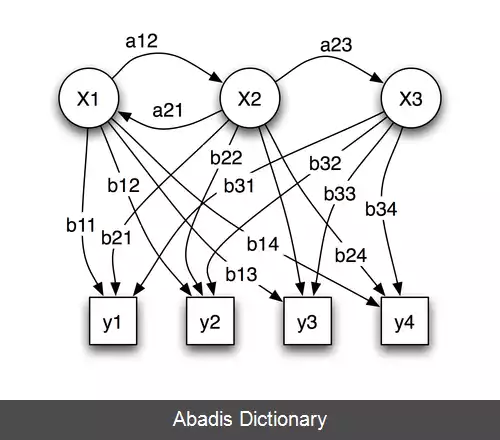
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر مدل عادی مارکوف، حالت به طور مستقیم توسط ناظر قابل مشاهده است و بنابراین احتمال های انتقال بین حالت ها تنها پارامترهای موجود است. در یک مدل پنهان مارکوف، حالت به طور مستقیم قابل مشاهده نیست، اما خروجی، بسته به حالت، قابل مشاهده است. هر حالت یک توزیع احتمال روی سمبل های خروجی ممکن دارد؛ بنابراین دنبالهٔ سمبل های تولید شده توسط یک مدل پنهان مارکوف اطلاعاتی دربارهٔ دنبالهٔ حالت ها می دهد. توجه داشته باشید که صفت 'پنهان' به دنبالهٔ حالت هایی که مدل از آن ها عبور می کند اشاره دارد، نه به پارامترهای مدل؛ حتی اگر پارامترهای مدل به طور دقیق مشخص باشند، مدل همچنان 'پنهان' است.
مدل های پنهان مارکوف بیشتر به دلیل کاربردشان در بازشناخت الگو، مانند تشخیص صدا و دست خط، تشخیص اشاره و حرکت، برچسب گذاری اجزای سخن، بیوانفورماتیک و … شناخته شده هستند.
مدل پنهان مارکوف در حالت گسسته جز خانوادهٔ مسائل ظرف ها قرار می گیرد. به طور مثال از ربینر ۱۹۸۹: ظروف x1، x2، x3. . . و توپهای رنگی y1, y2, y3… را در نظر می گیریم، که نفر مقابل دنباله ای از توپ ها را مشاهده کرده ولی اطلاعی از دنبالهٔ ظرف هایی که توپ ها از آن ها انتخاب شده ندارد. ظرف n ام با احتمالی وابسته به ظرف n - 1 ام انتخاب می شود و چون به انتخاب ظرف های خیلی قبل تر وابسته نیست یک فرایند مارکوف است.
شکل زیر معماری کلی یک نمونه HMM را نشان می دهد. هر شکل بیضی یک متغیر تصادفی است که می تواند هر عددی از مقادیر را انتخاب کند. متغیر تصادفی x ( t ) یک حالت پنهان در زمان t و متغیر تصادفی y ( t ) مشاهده در زمان t است. فلش ها به معنای وابستگی های شرطی می باشند. از شکل مشخص است که توزیع احتمال شرطی متغیر پنهان x ( t ) ، در همهٔ زمان هایt مقداری را برایx ارائه می دهد که فقط به مقدار متغیر پنهان x ( t − 1 ) وابسته است: مقادیر در زمان های t - 2 و قبل تر از آن هیچ اثری ندارند. این مشخصهٔ مارکف نامیده می شود. به طور مشابه، مقدار متغیر مشاهده ای y ( t ) تنها به مقدار متغیر پنهان x ( t ) ( هر دو در زمان خاص t ) بستگی دارد. در حالت استاندارد مدل پنهان مارکوف که در اینجا در نظر گرفته شده است، فضای حالت متغیرهای پنهان گسسته است؛ درحالی که متغیرهای مشاهده ای می توانند گسسته یا پیوسته ( از توزیع گوسین ) باشند.






wiki: مدل مارکوف پنهان
