مدل بلوکی تصادفی یک مدل تولیدی برای شبکه های تصادفی است. شبکه های تولید شده توسط این مدل شامل چندین اجتماع خواهند بود که زیرمجموعه هایی هستند که توزیع درجات رئوس مشابهی دارند. برای مثال ممکن است یال های بین رئوس در یک اجتماع بیشتر از اجتماعی دیگر باشند. مدل بلوکی تصادفی در آمار، یادگیری ماشین و علوم شبکه به عنوان یک معیار کارآمد برای شناسایی ساختارهای اجتماعی در اطلاعات مربوط به یک شبکه ( گراف ) اهمیت پیدا می کند.
یک مدل بلوکی تصادفی پارامترهای زیر را به عنوان ورودی دریافت می کند:
• تعداد رأس های شبکه ( n )
• یک بردار پارش شبکه به چندین اجتماع C 1 , … , C r {\displaystyle C_{1}, \ldots , C_{r}} که هر کدام از C i {\displaystyle C_{i}} ها نشان دهنده یک اجتماع هستند.
• یک ماتریس متقارن r × r {\displaystyle r\times r} به نام P حاوی احتمال اتصال یال ها
پس از دریافت این پارامترها، شبکه با فرایند زیر تشکیل می شود:
هر راس از اجتماع i به رأسی از اجتماع j با احتمالی که در المان i و j ماتریس P ( P i j ) داده شده است متصل می شود. ساختاری که شکل می گیرد به صورت بلوک های داده شده در بردار پارش خواهد بود.
در صورتی که ماتریس احتمال ثابت باشد، به عنوان مثال P i j = p برای تمامی i و jها، آن گاه شبکهٔ حاصل از این مدل یک گراف اردوش رنیی با تعداد رئوس n و احتمال اتصال p خواهد بود. این حالت خاص یک حالت تبهگن است، بدین صورت که تقسیم بندی شبکه به چند اجتماع عملاً بی معنی خواهد بود، اما ارتباط بین این دو مدل را نمایش می دهد.
مدل پارتیشن بندی انتصابی حالت خاص دیگری است که المان های قطری ماتریس احتمال ثابتی مانند p و المان های غیرقطری آن ثابتی دیگر مانند q هستند؛ بنابراین دو رأس در یک اجتماع با احتمال p با یک یال به هم متصل می شوند، در حالی که دو راس در دو اجتماع مختلف دارای یک یال با احتمال q خواهند بود. گاهی اوقات چیزی که به عنوان مدل بلوکی تصادفی شناخته می شود همین حالت خاص می باشد. حالتی که در آن p > q باشد یک مدل همگزین و حالتی که در آن p < q باشد ناهمگزین ( دیگرگزین ) نامیده می شود.
در حالت کلی مدل بلوکی تصادفی با ماتریس احتمال P i j ، یک شبکه همگزین قوی است در صورتی که P i i > P j k برای المان هایی که j و k برابر نیستند. به عبارت دیگر در شبکهٔ همگزین قوی، المان های قطری از همه المان های غیرقطری بزرگ تر هستند. همچنین یک شبکه همگزین ضعیف نام خواهد داشت اگر برای ماتریس احتمال آن برای i و jهای نابرابر داشته باشیم P i i > P i j . به عبارت دیگر در شبکهٔ همگزین ضعیف هر المان قطری تنها نیاز دارد تا از سایر المان های روی همان سطر و ستون بیشتر باشد. [ ۱] با برعکس کردن نامساوی ها تعریف حالت های ناهمگزین قوی و ضعیف بدست می آید. بازیابی ساختار اجتماع در شبکه ها اغلب در حالت های بلوکی با شرایط همگزینی یا ناهمگزینی از این نوع آسان تر است. [ ۱]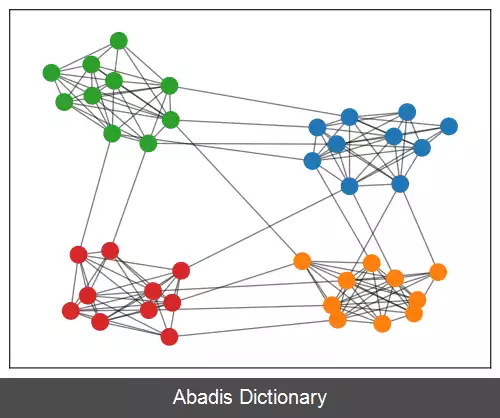
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک مدل بلوکی تصادفی پارامترهای زیر را به عنوان ورودی دریافت می کند:
• تعداد رأس های شبکه ( n )
• یک بردار پارش شبکه به چندین اجتماع C 1 , … , C r {\displaystyle C_{1}, \ldots , C_{r}} که هر کدام از C i {\displaystyle C_{i}} ها نشان دهنده یک اجتماع هستند.
• یک ماتریس متقارن r × r {\displaystyle r\times r} به نام P حاوی احتمال اتصال یال ها
پس از دریافت این پارامترها، شبکه با فرایند زیر تشکیل می شود:
هر راس از اجتماع i به رأسی از اجتماع j با احتمالی که در المان i و j ماتریس P ( P i j ) داده شده است متصل می شود. ساختاری که شکل می گیرد به صورت بلوک های داده شده در بردار پارش خواهد بود.
در صورتی که ماتریس احتمال ثابت باشد، به عنوان مثال P i j = p برای تمامی i و jها، آن گاه شبکهٔ حاصل از این مدل یک گراف اردوش رنیی با تعداد رئوس n و احتمال اتصال p خواهد بود. این حالت خاص یک حالت تبهگن است، بدین صورت که تقسیم بندی شبکه به چند اجتماع عملاً بی معنی خواهد بود، اما ارتباط بین این دو مدل را نمایش می دهد.
مدل پارتیشن بندی انتصابی حالت خاص دیگری است که المان های قطری ماتریس احتمال ثابتی مانند p و المان های غیرقطری آن ثابتی دیگر مانند q هستند؛ بنابراین دو رأس در یک اجتماع با احتمال p با یک یال به هم متصل می شوند، در حالی که دو راس در دو اجتماع مختلف دارای یک یال با احتمال q خواهند بود. گاهی اوقات چیزی که به عنوان مدل بلوکی تصادفی شناخته می شود همین حالت خاص می باشد. حالتی که در آن p > q باشد یک مدل همگزین و حالتی که در آن p < q باشد ناهمگزین ( دیگرگزین ) نامیده می شود.
در حالت کلی مدل بلوکی تصادفی با ماتریس احتمال P i j ، یک شبکه همگزین قوی است در صورتی که P i i > P j k برای المان هایی که j و k برابر نیستند. به عبارت دیگر در شبکهٔ همگزین قوی، المان های قطری از همه المان های غیرقطری بزرگ تر هستند. همچنین یک شبکه همگزین ضعیف نام خواهد داشت اگر برای ماتریس احتمال آن برای i و jهای نابرابر داشته باشیم P i i > P i j . به عبارت دیگر در شبکهٔ همگزین ضعیف هر المان قطری تنها نیاز دارد تا از سایر المان های روی همان سطر و ستون بیشتر باشد. [ ۱] با برعکس کردن نامساوی ها تعریف حالت های ناهمگزین قوی و ضعیف بدست می آید. بازیابی ساختار اجتماع در شبکه ها اغلب در حالت های بلوکی با شرایط همگزینی یا ناهمگزینی از این نوع آسان تر است. [ ۱]

wiki: مدل بلوکی تصادفی
