در تئوری سیستم های ذره ای ، مختصات یاکوبی اغلب برای ساده سازی فرمول ریاضی استفاده می شوند. این مختصات به ویژه در مولکولهای چند اتمی و واکنشهای شیمیایی ، [ ۱] و در مکانیک سماوی رایج است. [ ۲] یک الگو برای تولید مختصات یاکوبی برای N جسم ممکن است بر پایه درخت دودویی باشد. [ ۳] در کلمات ، الگو به شرح زیر است: [ ۳]
بگذارید m j و m k جرم دو جسم باشند که جسم جدیدی از جرم مجازی M = m j + m k جایگزین می شوند. مختصات موقعیت x j و x k با موقعیت نسبی آنها r jk = x j جایگزین می شوند − x k و توسط بردار به مرکز جرم آنها R jk = ( m j q j + m k q k ) / ( m j + m k ) . گره موجود در درخت دودویی که مربوط به جسم مجازی است m j را به عنوان فرزند راست خود و m k به عنوان فرزند چپ خود قرار داده است. منظور از کودکان نشان دهنده نسبی مختصات نقاط از x K به x J. مرحله بالا را برای N تکرار کنید − ۱ جسم ، یعنی ن − ۲ جسم اصلی به همراه جسم مجازی جدید.
برای مشکل بدن - ان نتیجه این است: [ ۶]
r j = 1 m 0 j ∑ k = 1 j m k x k − x j + 1 ( j = 1 , 2 , … , N − 1 )
r N = 1 m 0 N ∑ k = 1 N m k x k
با
m 0 j = ∑ k = 1 j m k .
بردار شکست در تجزیه ( پاسخ نامعتبر MathML همراه SVG یا PNG جایگزین ( توصیه شده برای مرورگرهای مدرن و ابزارهای کمکی ) ( " Math extension cannot connect to Restbase. " ) از سرور " http://localhost:6011/fa. wikipedia. org/v1/" : ) : {\displaystyle \boldsymbol{r_N} } مرکز جرم جسم است:
نتیجه ای که با آن باقی مانده است ، بنابراین یک سیستم از مختصات N - ۱ به طور ترجمه ای بی تحرک است r 1 , … , r N − 1 و یک مرکز هماهنگی جمعی r N ، از تکرار سیستمهای دو جسم در سیستم چند جسمی.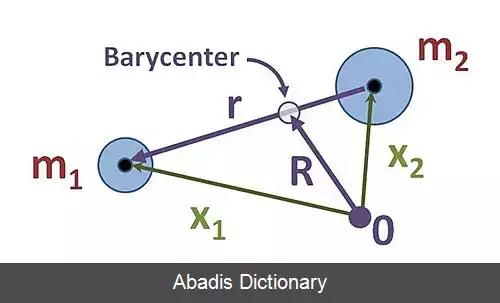
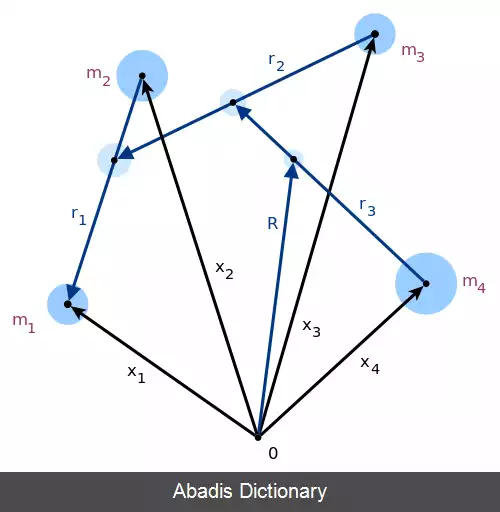
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبگذارید m j و m k جرم دو جسم باشند که جسم جدیدی از جرم مجازی M = m j + m k جایگزین می شوند. مختصات موقعیت x j و x k با موقعیت نسبی آنها r jk = x j جایگزین می شوند − x k و توسط بردار به مرکز جرم آنها R jk = ( m j q j + m k q k ) / ( m j + m k ) . گره موجود در درخت دودویی که مربوط به جسم مجازی است m j را به عنوان فرزند راست خود و m k به عنوان فرزند چپ خود قرار داده است. منظور از کودکان نشان دهنده نسبی مختصات نقاط از x K به x J. مرحله بالا را برای N تکرار کنید − ۱ جسم ، یعنی ن − ۲ جسم اصلی به همراه جسم مجازی جدید.
برای مشکل بدن - ان نتیجه این است: [ ۶]
r j = 1 m 0 j ∑ k = 1 j m k x k − x j + 1 ( j = 1 , 2 , … , N − 1 )
r N = 1 m 0 N ∑ k = 1 N m k x k
با
m 0 j = ∑ k = 1 j m k .
بردار شکست در تجزیه ( پاسخ نامعتبر MathML همراه SVG یا PNG جایگزین ( توصیه شده برای مرورگرهای مدرن و ابزارهای کمکی ) ( " Math extension cannot connect to Restbase. " ) از سرور " http://localhost:6011/fa. wikipedia. org/v1/" : ) : {\displaystyle \boldsymbol{r_N} } مرکز جرم جسم است:
نتیجه ای که با آن باقی مانده است ، بنابراین یک سیستم از مختصات N - ۱ به طور ترجمه ای بی تحرک است r 1 , … , r N − 1 و یک مرکز هماهنگی جمعی r N ، از تکرار سیستمهای دو جسم در سیستم چند جسمی.


wiki: مختصات یاکوبی
