مجموعه کانتور در ریاضیات مجموعه ای از نقاط است که به روی یک پاره خط واحد که دارای خواص ویژه ای است قرار گرفته اند. این مجموعه در سال ۱۸۷۴ توسط هنری جان استفن اسمیت شناخته شد و در سال ۱۸۸۳ به وسیله گئورگ کانتور معرفی گردید. اگر چه خود کانتور مجموعه را به طور عمومی و انتزاعی تعریف کرد اما رایج ترین و مدرن ترین ساختار، مجموعه کانتور سه تایی است که به وسیلهٔ تقسیم پاره خط به سه قسمت و برداشتن قسمت وسط ساخته می شود.
مجموعه کانتور سه تایی به این صورت ساخته می شود که به طور مداوم پاره خط را به سه قسمت تقسیم کرده و قسمت وسط را برداریم. مثلاً درفاصلهٔ مرحلهٔ اول برداشتن بازهٔ ( ۲⁄۳، ۱⁄۳ ) است که در این صورت ∪ باقی می ماند. در مرحلهٔ بعد این کار بر روی بازه های باقی مانده تکرار می شود. در این جا داریم: ∪ ∪ ∪ . این روند تا بی نهایت ادامه پیدا می کند و مجموعهٔ nام برابر می شود با: C n = C n − 1 3 ∪ ( 2 3 + C n − 1 3 ) . مجموعه کانتور سه تایی تمام نقاط بازهٔ که در این روند حذف نشده اند را داراست. ۶ مرحلهٔ اول این روند در زیر نشان داده شده است: فرمول دقیق مجموعه کانتور برابر است با: C = ∖ ⋃ m = 1 ∞ ⋃ k = 0 3 m − 1 − 1 ( 3 k + 1 3 m , 3 k + 2 3 m ) .
چون مجموعه کانتور مجموعه ای از نقاط تعریف می شود مقدار فاصلهٔ واحد باقی مانده را می توان با کم کردن طول کل پیدا کرد. مجموع یک تصاعد هندسی است. ∑ n = 0 ∞ 2 n 3 n + 1 = 1 3 + 2 9 + 4 27 + 8 81 + ⋯ = 1 3 ( 1 1 − 2 3 ) = 1.
بنابراین مقدار باقی مانده برابر است با: 1 – 1 = ۰ این محاسبه نشان می دهد که مجموعه کانتور نمی تواند هیچ بازه ای با طول غیر صفر را در بر بگیرد. در واقع ممکن است عجیب به نظر برسد که چیزی باقی بماند چون مجموع طول بازه های حذف شده برابر با طول بازهٔ اصلی است. با این وجود نگاه دقیق تر به روند نشان می دهد که باید چیزی باقی مانده باشد. از ان جا که برداشتن وسط سه قسمت از مجموعه های باز ( مجموعه ای که نقاط پایانی ان مشخص نیست ) انجام می گیرد بنابراین با برداشتن پاره خط ( ۲⁄۳، ۱⁄۳ ) از بازهٔ دو نقطهٔ ۱/۳ و ۲/۳ باقی می مانند. باقی مراحل این نقاط پایانی را خارج نمی کنند. از انجا که بازه های حذف شده همیشه برای بازه های باقی مانده داخلی هستند بنابراین مجموعه کانتور تهی نیست و در واقع شامل تعداد نامحدود از نقاط است. ممکن است این طور به نظر برسد که فقط نقاط پایانی باقی می مانند اما این گونه نیست. برای مثال نقطهٔ ۱/۴ در یک سوم ابتدایی قرار دارد و در مرحلهٔ اول حذف نمی شود. در مرحله دوم در یک سوم انتهایی، سپس در یک سوم ابتدایی و به همین ترتیب این روند تا بی نهایت بین یک سوم ابتدایی و انتهایی ادامه دارد. از انجا که این عدد هیچ گاه در یک سوم وسط قرار نمی گیرد، هیچ وقت حذف نمی شود و همچنین هیچ یک از نقاط پایانی یک سوم وسط هم نیست. عدد۳/۱۰ نیز به همین شکل در مجموعه کانتور قرار دارد و جز نقاط پایانی هم نیست. در کاردینال بیشتر اعضای مجموعه کانتور نقاط پایانی بازه های حذف شده نیستند.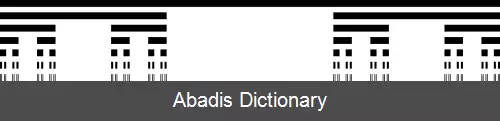
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمجموعه کانتور سه تایی به این صورت ساخته می شود که به طور مداوم پاره خط را به سه قسمت تقسیم کرده و قسمت وسط را برداریم. مثلاً درفاصلهٔ مرحلهٔ اول برداشتن بازهٔ ( ۲⁄۳، ۱⁄۳ ) است که در این صورت ∪ باقی می ماند. در مرحلهٔ بعد این کار بر روی بازه های باقی مانده تکرار می شود. در این جا داریم: ∪ ∪ ∪ . این روند تا بی نهایت ادامه پیدا می کند و مجموعهٔ nام برابر می شود با: C n = C n − 1 3 ∪ ( 2 3 + C n − 1 3 ) . مجموعه کانتور سه تایی تمام نقاط بازهٔ که در این روند حذف نشده اند را داراست. ۶ مرحلهٔ اول این روند در زیر نشان داده شده است: فرمول دقیق مجموعه کانتور برابر است با: C = ∖ ⋃ m = 1 ∞ ⋃ k = 0 3 m − 1 − 1 ( 3 k + 1 3 m , 3 k + 2 3 m ) .
چون مجموعه کانتور مجموعه ای از نقاط تعریف می شود مقدار فاصلهٔ واحد باقی مانده را می توان با کم کردن طول کل پیدا کرد. مجموع یک تصاعد هندسی است. ∑ n = 0 ∞ 2 n 3 n + 1 = 1 3 + 2 9 + 4 27 + 8 81 + ⋯ = 1 3 ( 1 1 − 2 3 ) = 1.
بنابراین مقدار باقی مانده برابر است با: 1 – 1 = ۰ این محاسبه نشان می دهد که مجموعه کانتور نمی تواند هیچ بازه ای با طول غیر صفر را در بر بگیرد. در واقع ممکن است عجیب به نظر برسد که چیزی باقی بماند چون مجموع طول بازه های حذف شده برابر با طول بازهٔ اصلی است. با این وجود نگاه دقیق تر به روند نشان می دهد که باید چیزی باقی مانده باشد. از ان جا که برداشتن وسط سه قسمت از مجموعه های باز ( مجموعه ای که نقاط پایانی ان مشخص نیست ) انجام می گیرد بنابراین با برداشتن پاره خط ( ۲⁄۳، ۱⁄۳ ) از بازهٔ دو نقطهٔ ۱/۳ و ۲/۳ باقی می مانند. باقی مراحل این نقاط پایانی را خارج نمی کنند. از انجا که بازه های حذف شده همیشه برای بازه های باقی مانده داخلی هستند بنابراین مجموعه کانتور تهی نیست و در واقع شامل تعداد نامحدود از نقاط است. ممکن است این طور به نظر برسد که فقط نقاط پایانی باقی می مانند اما این گونه نیست. برای مثال نقطهٔ ۱/۴ در یک سوم ابتدایی قرار دارد و در مرحلهٔ اول حذف نمی شود. در مرحله دوم در یک سوم انتهایی، سپس در یک سوم ابتدایی و به همین ترتیب این روند تا بی نهایت بین یک سوم ابتدایی و انتهایی ادامه دارد. از انجا که این عدد هیچ گاه در یک سوم وسط قرار نمی گیرد، هیچ وقت حذف نمی شود و همچنین هیچ یک از نقاط پایانی یک سوم وسط هم نیست. عدد۳/۱۰ نیز به همین شکل در مجموعه کانتور قرار دارد و جز نقاط پایانی هم نیست. در کاردینال بیشتر اعضای مجموعه کانتور نقاط پایانی بازه های حذف شده نیستند.

wiki: مجموعه کانتور
