مجموعه چیره یا مجموعه غالب یا مجموعه احاطه گری برای گراف ( G= ( V, E زیرمجموعه ای از گره هاست به گونه ای که هر گره یا درون این مجموعه است یا همسایه ای در این مجموعه دارد. شمار گره های کوچکترین مجموعه چیره را عدد چیرگی گراف می نامیم. یافتن مجموعه چیره ای برای گراف G و با عدد چیرگی Y ( G ) کوچک تر از K ∈ R مسئله ای ان پی سخت است ( Grandoni 2006 ) . بنابراین تاکنون الگوریتم بهینه ای برای یافتن این مجموعه چیره پیدا نشده است.
سه مجموعه چیرهٔ برای گرافی نمونه در شکل های a تا c نشان داده شده اند. هر گره قرمز همسایهٔ گره ای سفید است و به اصطلاح بر گره سفید چیره شده است. عدد چیرگی در این نمونه ها برابر ۲ است. هم چنین، به آسانی می توان نشان داد که هیچ یک از مجموعه های تک گره ای چیره نیستند.
پژوهش ها دربارهٔ مجموعهٔ چیره از دههٔ ۱۹۵۰ آغاز شدند و در میانهٔ ۱۹۷۰ با به اوج رسیدن پژوهش ها بیش از ۳۰۰ جستار در این زمینه نوشته شد. [ ۱]
این مسئله کاربردهای بسیاری در زمینهٔ مسیریابی و رایانش های توزیع شده یا خوشه ای دارد. برای نمونه در یک شبکه، فرستادنِ پلکانی پیام از خوشه ای به خوشهٔ دیگری می تواند از راه سرخوشه ها انجام شود. سرخوشه گره ای است که مسیریابی درون و میان خوشه ای را انجام می دهد. پرسش اینجاست که برای چنین شبکه ای کدام گره ها باید برای سرخوشگی برگزیده شوند تا بتوان از هر خوشه ای به خوشه ای دیگر پیام فرستاد و هم چنین، کم ترین سرخوشه ها را داشته باشیم. یافتن مجموعهٔ چیرهٔ کمینه برای چنین شبکه ای هم ارز است با یافتن کم ترین شمار سرخوشه ها.
برای گراف G دارای n ≥ 1 گره و با بیشینه درجه Δ ، نابرابری های زیر را برای عدد چیرگی Y ( G ) داریم:[ ۲]
• یک گره می تواند دست بالا بر Δ {\displaystyle \Delta } گرهٔ دیگر چیره شود؛ بنابراین Y ( G ) ≥ n 1 + Δ {\displaystyle Y ( G ) \geq {\frac {n}{1+\Delta }}} .
• مجموعه همه گره ها در هر گراف یک مجموعه چیره است، از این رو Y ( G ) ≤ n {\displaystyle Y ( G ) \leq n} .
• اگر هیچ گرهٔ تنهایی در گراف نباشد، آن گاه دو مجموعه چیرهٔ سوا ( disjoint ) برای گراف خواهیم داشت؛ بنابراین در هر گرافی بدون گره ای تنها داریم Y ( G ) ≤ n 2 {\displaystyle Y ( G ) \leq {\frac {n}{2}}} .
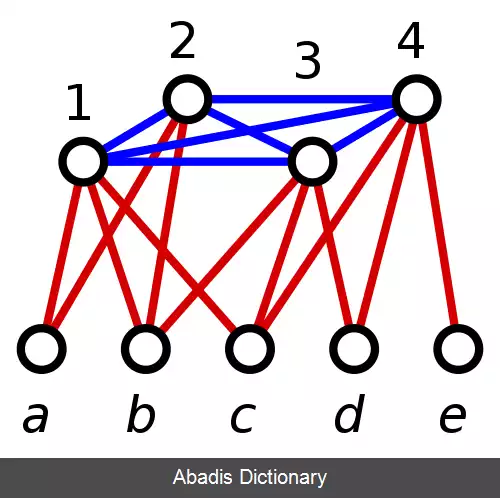
مجموعه های چیره پیوند نزدیکی با مجموعه های ناوابسته در گراف دارند. مجموعه ای ناوابسته یک مجموعه چیره نیز است اگر و تنها اگر یک مجموعه ناوابسته بیشینه باشد؛ بنابراین هر مجموعه ناوابسته بیشینه مجموعه ای چیرهٔ کمینه است. پس کوچکترین مجموعه ناوابسته بیشینه بی گمان کوچک ترین مجموعه چیره ناوابسته خواهد بود. اندازه کوچک ترین مجموعه چیره ناوابسته ( یا همان گونه که گفته شد کوچکترین مجموعه ناوابسته بیشینه ) عدد چیرگی ناوابسته نامیده و با i ( G ) می شود. کوچک ترین مجموعه چیره در گرافی بی گمان یک مجموعه ناوابسته نخواهد بود ولی اندازه آن همیشه کوچکتر یا برابر اندازه کوچکترین مجموعه ناوابسته بیشینه است: Y ( G ) ≤ i ( G ) .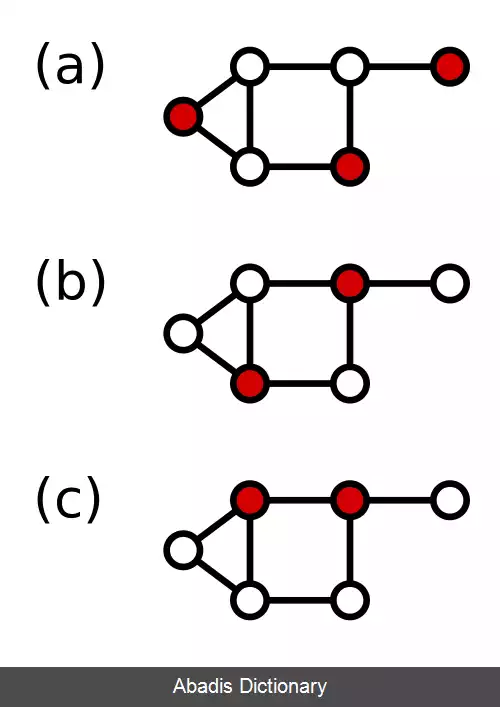
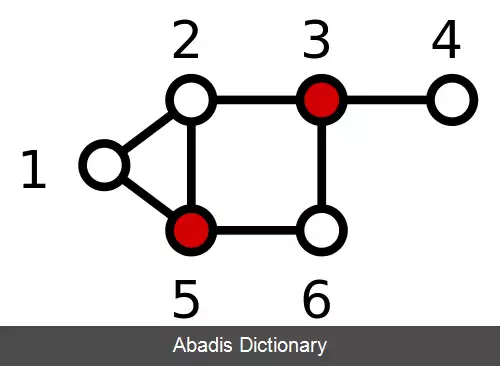
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفسه مجموعه چیرهٔ برای گرافی نمونه در شکل های a تا c نشان داده شده اند. هر گره قرمز همسایهٔ گره ای سفید است و به اصطلاح بر گره سفید چیره شده است. عدد چیرگی در این نمونه ها برابر ۲ است. هم چنین، به آسانی می توان نشان داد که هیچ یک از مجموعه های تک گره ای چیره نیستند.
پژوهش ها دربارهٔ مجموعهٔ چیره از دههٔ ۱۹۵۰ آغاز شدند و در میانهٔ ۱۹۷۰ با به اوج رسیدن پژوهش ها بیش از ۳۰۰ جستار در این زمینه نوشته شد. [ ۱]
این مسئله کاربردهای بسیاری در زمینهٔ مسیریابی و رایانش های توزیع شده یا خوشه ای دارد. برای نمونه در یک شبکه، فرستادنِ پلکانی پیام از خوشه ای به خوشهٔ دیگری می تواند از راه سرخوشه ها انجام شود. سرخوشه گره ای است که مسیریابی درون و میان خوشه ای را انجام می دهد. پرسش اینجاست که برای چنین شبکه ای کدام گره ها باید برای سرخوشگی برگزیده شوند تا بتوان از هر خوشه ای به خوشه ای دیگر پیام فرستاد و هم چنین، کم ترین سرخوشه ها را داشته باشیم. یافتن مجموعهٔ چیرهٔ کمینه برای چنین شبکه ای هم ارز است با یافتن کم ترین شمار سرخوشه ها.
برای گراف G دارای n ≥ 1 گره و با بیشینه درجه Δ ، نابرابری های زیر را برای عدد چیرگی Y ( G ) داریم:[ ۲]
• یک گره می تواند دست بالا بر Δ {\displaystyle \Delta } گرهٔ دیگر چیره شود؛ بنابراین Y ( G ) ≥ n 1 + Δ {\displaystyle Y ( G ) \geq {\frac {n}{1+\Delta }}} .
• مجموعه همه گره ها در هر گراف یک مجموعه چیره است، از این رو Y ( G ) ≤ n {\displaystyle Y ( G ) \leq n} .
• اگر هیچ گرهٔ تنهایی در گراف نباشد، آن گاه دو مجموعه چیرهٔ سوا ( disjoint ) برای گراف خواهیم داشت؛ بنابراین در هر گرافی بدون گره ای تنها داریم Y ( G ) ≤ n 2 {\displaystyle Y ( G ) \leq {\frac {n}{2}}} .
مجموعه های چیره پیوند نزدیکی با مجموعه های ناوابسته در گراف دارند. مجموعه ای ناوابسته یک مجموعه چیره نیز است اگر و تنها اگر یک مجموعه ناوابسته بیشینه باشد؛ بنابراین هر مجموعه ناوابسته بیشینه مجموعه ای چیرهٔ کمینه است. پس کوچکترین مجموعه ناوابسته بیشینه بی گمان کوچک ترین مجموعه چیره ناوابسته خواهد بود. اندازه کوچک ترین مجموعه چیره ناوابسته ( یا همان گونه که گفته شد کوچکترین مجموعه ناوابسته بیشینه ) عدد چیرگی ناوابسته نامیده و با i ( G ) می شود. کوچک ترین مجموعه چیره در گرافی بی گمان یک مجموعه ناوابسته نخواهد بود ولی اندازه آن همیشه کوچکتر یا برابر اندازه کوچکترین مجموعه ناوابسته بیشینه است: Y ( G ) ≤ i ( G ) .



wiki: مجموعه چیره
