مجموعهٔ مندلبرو ( به انگلیسی: Mandelbrot set ) مجموعه ای از نقطه ها روی صفحهٔ مختلط است که یک فراکتال را تشکیل می دهند. این مجموعه به خاطر زیبایی اش و نیز به خاطر ساختار پیچیده ای که فقط از چند تعریف سادهٔ ریاضی ناشی شده ، در بیرون از دنیای ریاضیات هم شناخته شده می باشد.
مجموعهٔ مندلبرو اولین بار توسط یک ریاضی دان فرانسوی به نام پیر فاتو که در زمینه آنالیز مختلط پویا فعالیت می کرد در سال ۱۹۰۵ تعریف شد. فاتو در آن زمان به کامپیوتر مستعد برای ترسیم این تابع دسترسی نداشت و با وجود محاسبات زیاد نتوانست اشکالی را که ما امروزه می بینیم ببیند. هم زمان ریاضی دان دیگری به نام ژولیا روی توابع گویا روی صفحهٔ اعداد مختلط کار می کرد. امروز مجموعه های ژولیا از شکل های معروف فرکتالی است. این مباحث به صورت موضوعاتی پراکنده مطرح بودند تا این که بنوا مندلبرو در سال ۱۹۷۹ با انتشار مقالهٔ Fractals: Form, chance and dimension مباحث فوق و بسیاری از مباحث دیگر را تحت عنوان هندسه فرکتالی جمع بندی و عرضه کرد و با انتشار کتاب هندسه فرکتالی طبیعت توسط مندلبرو عملاً شکوفایی هندسهٔ فرکتالی آغاز شد.
مجموعه مندلبرو M ، مرکب از «c - مقدارهای» مختلطی ست که دنبالهٔ حاصل از تکرار ترکیب تابع f c ( z ) = z 2 + c با خودش در نقطهٔ آغازین صفر به بینهایت میل نکند.
در آنالیز پویا اصطلاحاً به دنباله ای از نقاط که از تکرار ترکیب یک تابع با خودش به دست می آید ابر یا اربیت نقاط تحت آن تابع می گویند. به بیانی دیگر مجموعه مندلبرو مجموعه نقاط اربیت های بدست آمده تحت تابع z 2 + c است که به بینهایت نمی گراید.
• قضیه ( ملاک میل به بی نهایت به انگلیسی The Escape Criterion ) : فرض کنید c {\displaystyle c} عضوی از مجموعه مندلبرو است اگر و تنها اگر اربیت تحت x 2 + c {\displaystyle x^{2}+c} از دایره ای به شعاع ۲ و به مرکز مبدأ خارج نشود. ( بیان دیگر به ازای | c | > 2 {\displaystyle |c|> 2} اربیت تحت x 2 + c {\displaystyle x^{2}+c} به بی نهایت میل می کند )
این قضیه نشان می دهد مجموعه مندلبرو کاملاً در داخل دیسک به شعاع ۲ قرار دارد.
این مجموعه در صفحه مختلط C فشرده است. همچنین دو ریاضی دان به نام های دوادی و هابارد اثبات کرده اند که این مجموعه در صفحه C پیوسته است
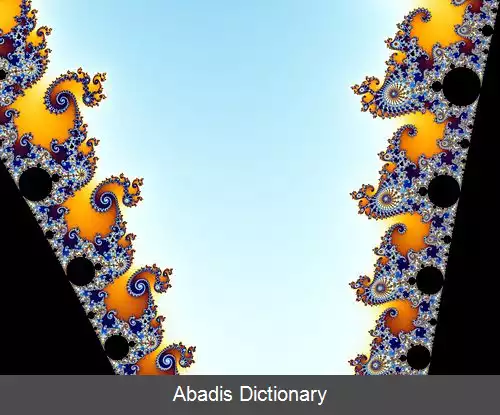
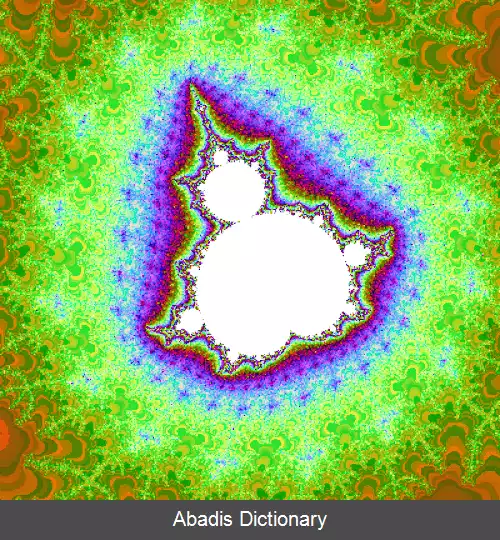
برای خلق آثار زیبای بصری رایانه ای از این فرکتال، از رنگ آمیزی های مختلف استفاده می شود و اساس آن مرتبهٔ تکرّر ( iteration ) است به طوری که در هر تکرار در صورت تشخیص خارج بودن نقاط از مجموعه به آن نقاط رنگ مربوط به مرتبه تکرار تعلق می گیرد. به این ترتیب تصاویر رنگی به وجود می آید.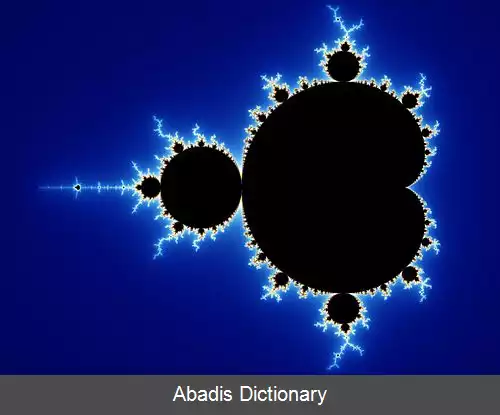



این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمجموعهٔ مندلبرو اولین بار توسط یک ریاضی دان فرانسوی به نام پیر فاتو که در زمینه آنالیز مختلط پویا فعالیت می کرد در سال ۱۹۰۵ تعریف شد. فاتو در آن زمان به کامپیوتر مستعد برای ترسیم این تابع دسترسی نداشت و با وجود محاسبات زیاد نتوانست اشکالی را که ما امروزه می بینیم ببیند. هم زمان ریاضی دان دیگری به نام ژولیا روی توابع گویا روی صفحهٔ اعداد مختلط کار می کرد. امروز مجموعه های ژولیا از شکل های معروف فرکتالی است. این مباحث به صورت موضوعاتی پراکنده مطرح بودند تا این که بنوا مندلبرو در سال ۱۹۷۹ با انتشار مقالهٔ Fractals: Form, chance and dimension مباحث فوق و بسیاری از مباحث دیگر را تحت عنوان هندسه فرکتالی جمع بندی و عرضه کرد و با انتشار کتاب هندسه فرکتالی طبیعت توسط مندلبرو عملاً شکوفایی هندسهٔ فرکتالی آغاز شد.
مجموعه مندلبرو M ، مرکب از «c - مقدارهای» مختلطی ست که دنبالهٔ حاصل از تکرار ترکیب تابع f c ( z ) = z 2 + c با خودش در نقطهٔ آغازین صفر به بینهایت میل نکند.
در آنالیز پویا اصطلاحاً به دنباله ای از نقاط که از تکرار ترکیب یک تابع با خودش به دست می آید ابر یا اربیت نقاط تحت آن تابع می گویند. به بیانی دیگر مجموعه مندلبرو مجموعه نقاط اربیت های بدست آمده تحت تابع z 2 + c است که به بینهایت نمی گراید.
• قضیه ( ملاک میل به بی نهایت به انگلیسی The Escape Criterion ) : فرض کنید c {\displaystyle c} عضوی از مجموعه مندلبرو است اگر و تنها اگر اربیت تحت x 2 + c {\displaystyle x^{2}+c} از دایره ای به شعاع ۲ و به مرکز مبدأ خارج نشود. ( بیان دیگر به ازای | c | > 2 {\displaystyle |c|> 2} اربیت تحت x 2 + c {\displaystyle x^{2}+c} به بی نهایت میل می کند )
این قضیه نشان می دهد مجموعه مندلبرو کاملاً در داخل دیسک به شعاع ۲ قرار دارد.
این مجموعه در صفحه مختلط C فشرده است. همچنین دو ریاضی دان به نام های دوادی و هابارد اثبات کرده اند که این مجموعه در صفحه C پیوسته است
برای خلق آثار زیبای بصری رایانه ای از این فرکتال، از رنگ آمیزی های مختلف استفاده می شود و اساس آن مرتبهٔ تکرّر ( iteration ) است به طوری که در هر تکرار در صورت تشخیص خارج بودن نقاط از مجموعه به آن نقاط رنگ مربوط به مرتبه تکرار تعلق می گیرد. به این ترتیب تصاویر رنگی به وجود می آید.






wiki: مجموعه مندلبرو
