مجموعه مستقل ( به انگلیسی: Independent Set ) ، برای یک گراف مجموعه ای از گره ها ست که هیچ یالی میان هیچ جفتی از این گره ها نباشد.
مجموعهٔ مستقل بیشین، مجموعه ای مستقل است که با افزودن گره ای دیگر به این مجموعه دیگر مستقل نباشد. به سخنی دیگر، با افزودن گره ای دیگر، دو گره از این مجموعه همسایه خواهند بود.
برای گراف G ، مجموعهٔ مستقل بیشینه بیش ترین گره های ناهمسایهٔ این گراف را دارد و اندازهٔ این مجموعه با α ( G ) نشان داده می شود. هر مجموعهٔ ناوابستهٔ بیشینه ای مجموعه ای وابستهٔ بیشین نیز هست، ولی مجموعه ای ناوابستهٔ بیشین بایستانه ( به لزوم ) بیشینه نیست. یافتن مجموعهٔ ناوابستهٔ بیشینه پرسمانی ان پی سخت است. از این روی نمی توان در زمانی کوتاه چنین مجموعه ای را یافت.
مجموعه ای مستقل است اگر و تنها اگر گروهکی باشد برای مکمل ( به انگلیسی: complement ) گراف. این گزاره بدین معناست که برای گراف هایی بزرگ که گروهک هایی بزرگ نداشته باشند دارای مجموعه های ناوابستهٔ بزرگی خواهند بود. نظریه رمزی چنین شیوه ای را بررسی کرده است.
مجموعه ای مستقل است اگر و تنها اگر اُسپُران این مجموعه یک پوشش گره باشد. از همین روی اندازهٔ بزرگترین مجموعهٔ مستقل و اندازهٔ کوچک ترین پوشش گره ای برابرند با شمار گره های گراف باشد.
مسئلهٔ یافتن یک مجموعهٔ مستقل بیشین را می توان در زمان چندجمله ای به کمک یک الگوریتم حریصانه حل کرد. همهٔ مجموعه های مستقل بیشین را می توان در زمان ( O ( 3n/3 یافت.
مجموعهٔ مستقل در گراف و علم کامپیوتر کاربردهای بسیاری دارد و حتی جزء دسته مسئله های NP - complete محسوب می شود. در حالت کلی و برای یک گراف دلخواه تا به حال الگوریتمی چند جمله ای برای یافتن مجموعه مستقل پیدا نشده است. این مسائل NP - complete قابل تبدیل به یک دیگر هستند. برای اولین بار این تبدیل ها توسط کوک انجام شد.
برای حالت خاصی از گراف ها مجموعهٔ مستقل در زمان چند جمله ای قابل یافتن است. این دسته از گراف ها، گراف های دوبخشی هستند؛ به کمک الگوریتم تطابق می توانیم مجموعهٔ مورد نظر را پیدا کنیم.
G گرافی دوبخشی شامل دو بخش S۱ و S۲ است؛
• n: شمار گره ها G
• m: اندازهٔ تطابق بیشینه در G
لم: اندازهٔ مجموعهٔ مستقل بیشینه در G برابر n - m است.
برهان: برهان خلف؛ اگر مجموعهٔ ناوابستهٔ با اندازه ای بزرگتر از n - m وجود داشته باشد، دست کم دو گره که در تطابق بیشینه مجاور بودند، انتخاب شده اند. در نتیجه در این مجموعه یال وجود دارد. پس این مجموعه مستقل نیست.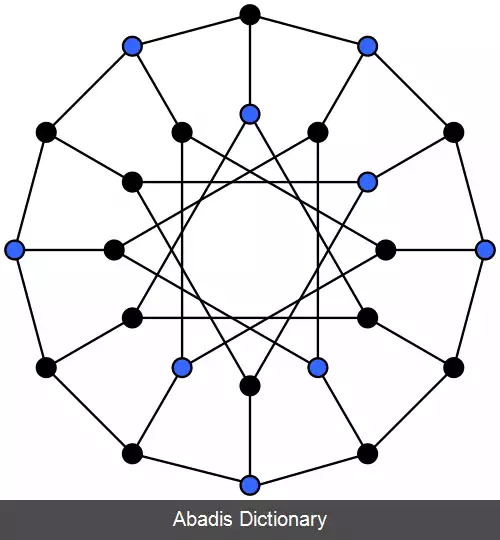
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمجموعهٔ مستقل بیشین، مجموعه ای مستقل است که با افزودن گره ای دیگر به این مجموعه دیگر مستقل نباشد. به سخنی دیگر، با افزودن گره ای دیگر، دو گره از این مجموعه همسایه خواهند بود.
برای گراف G ، مجموعهٔ مستقل بیشینه بیش ترین گره های ناهمسایهٔ این گراف را دارد و اندازهٔ این مجموعه با α ( G ) نشان داده می شود. هر مجموعهٔ ناوابستهٔ بیشینه ای مجموعه ای وابستهٔ بیشین نیز هست، ولی مجموعه ای ناوابستهٔ بیشین بایستانه ( به لزوم ) بیشینه نیست. یافتن مجموعهٔ ناوابستهٔ بیشینه پرسمانی ان پی سخت است. از این روی نمی توان در زمانی کوتاه چنین مجموعه ای را یافت.
مجموعه ای مستقل است اگر و تنها اگر گروهکی باشد برای مکمل ( به انگلیسی: complement ) گراف. این گزاره بدین معناست که برای گراف هایی بزرگ که گروهک هایی بزرگ نداشته باشند دارای مجموعه های ناوابستهٔ بزرگی خواهند بود. نظریه رمزی چنین شیوه ای را بررسی کرده است.
مجموعه ای مستقل است اگر و تنها اگر اُسپُران این مجموعه یک پوشش گره باشد. از همین روی اندازهٔ بزرگترین مجموعهٔ مستقل و اندازهٔ کوچک ترین پوشش گره ای برابرند با شمار گره های گراف باشد.
مسئلهٔ یافتن یک مجموعهٔ مستقل بیشین را می توان در زمان چندجمله ای به کمک یک الگوریتم حریصانه حل کرد. همهٔ مجموعه های مستقل بیشین را می توان در زمان ( O ( 3n/3 یافت.
مجموعهٔ مستقل در گراف و علم کامپیوتر کاربردهای بسیاری دارد و حتی جزء دسته مسئله های NP - complete محسوب می شود. در حالت کلی و برای یک گراف دلخواه تا به حال الگوریتمی چند جمله ای برای یافتن مجموعه مستقل پیدا نشده است. این مسائل NP - complete قابل تبدیل به یک دیگر هستند. برای اولین بار این تبدیل ها توسط کوک انجام شد.
برای حالت خاصی از گراف ها مجموعهٔ مستقل در زمان چند جمله ای قابل یافتن است. این دسته از گراف ها، گراف های دوبخشی هستند؛ به کمک الگوریتم تطابق می توانیم مجموعهٔ مورد نظر را پیدا کنیم.
G گرافی دوبخشی شامل دو بخش S۱ و S۲ است؛
• n: شمار گره ها G
• m: اندازهٔ تطابق بیشینه در G
لم: اندازهٔ مجموعهٔ مستقل بیشینه در G برابر n - m است.
برهان: برهان خلف؛ اگر مجموعهٔ ناوابستهٔ با اندازه ای بزرگتر از n - m وجود داشته باشد، دست کم دو گره که در تطابق بیشینه مجاور بودند، انتخاب شده اند. در نتیجه در این مجموعه یال وجود دارد. پس این مجموعه مستقل نیست.

wiki: مجموعه مستقل
